同軸度/同心度の記号は「◎(同心2円)」と覚える
グローバルで通用する図面を描くには、幾何公差の理解が欠かせません。
第15回となる今回は、「同軸度」と「同心度」に焦点を当て、これらが図面上でどのような意味をもち、どのように記号で表現されるのかを解説します。
回転体や組み立て部品の精度に直結するこの幾何公差は、設計者と製造者の間での認識ズレを防ぐためにも、正しく理解しておきたい重要なポイントです。具体例を交えながら、図面ルールの基本を押さえていきましょう。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >
目次
1.位置偏差とは
前回の5つの姿勢偏差に続いて、5種類ある位置偏差の詳細について解説していきます。
今回は、位置偏差というグループに含まれる同軸度・同心度です。
位置偏差は関連形体に分類され、データムに関連して幾何偏差が決められる形体になります。
位置偏差には次の5つの幾何特性があります。
・同軸度/同心度 ←今回解説する幾何特性
・対称度
・位置度
・線の輪郭度…位置偏差の場合、データムに関連する
・面の輪郭度…位置偏差の場合、データムに関連する
2.同軸度/同心度とは
同軸度は「データム軸直線と同一直線上にあるべき“軸線”のデータム軸直線からの狂いの大きさ」とJISで規定されます。
同心度は「データム軸直線と同一直線上にあるべき“点”のデータム軸直線からの狂いの大きさ」とJISで規定されます。
つまり、同軸度と同心度の違いは、検査対象が長さのある中心線か、長さのない中心点かの違いによるもので、記入の際は同じ記号「◎」を使用します。
同軸度/同心度は位置偏差のグループに属するためデータムを必要とします。
3.同軸度/同心度の記号と記入のルール
同軸度/同心度を図面に表現する場合、公差記入枠に同軸度/同心度の記号と幾何公差値、必要に応じてその他の記号、データム記号を記入します。同軸度/同心度を定義するにはデータムが1つだけあれば十分なため、公差記入枠は3つの区画のものを使います(図15-1)。

図15-1 同軸度/同心度の記入例
同軸度/同心度の対象となる形体は1本の中心線または1つの中心点です。従って、それらの形体を包み込む空間が公差領域となります。公差領域は回転方向の自由度がフリーとなるため幾何公差値に必ずφが付きます(図15-2)。
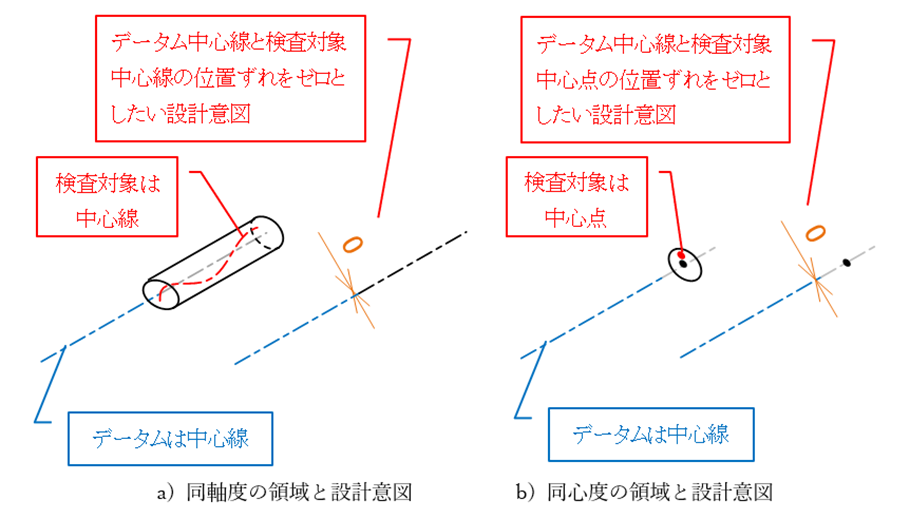
図15-2 同軸度/同心度の公差領域のパターン
4.同軸度/同心度を適用する形状
同軸度/同心度を適用する形状は、一般的に円筒形状や円筒穴に指示します(表15-1)。
表15-1 同軸度/同心度を適用する形状例
| 適用する形状例 | データム | 対象形体 | 補助記号 | ||
| 1
|
同一直線上の中心線 | 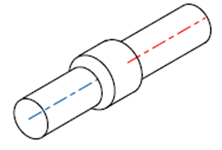
|
要
|
中心線
|
–
|
| 断続中心線
(同一中心線) |
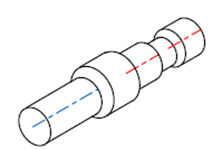 |
(断続形体) | (CZ) | ||
| 2 | 外径と同軸の穴
断続中心線 (同一中心線) |
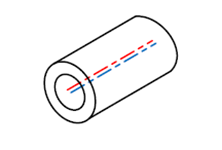 |
要 | 中心線
(断続形体) |
–
(CZ) |
| 3 | 外径と同心の穴
|
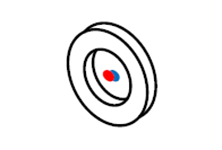 |
要 | 中心点
|
– |
5.同軸度/同心度の目的
同軸度/同心度は加工上ずれが生じやすく設計機能上必要という目的に加えて、加工者にどの程度の同軸を要求しているのかという加工者へのメッセージにもなります。
特に4つ爪チャックをもつ旋盤で加工する場合、丸棒をチャックに固定した時点で丸棒の中心線は旋盤の回転中心とずれます。この状態で丸棒を切削すると、切削部は旋盤の回転中心に倣(なら)いますが、チャックしている円筒部は偏芯したままですので、偏芯した段付き軸が出来上がります(図15-3)。
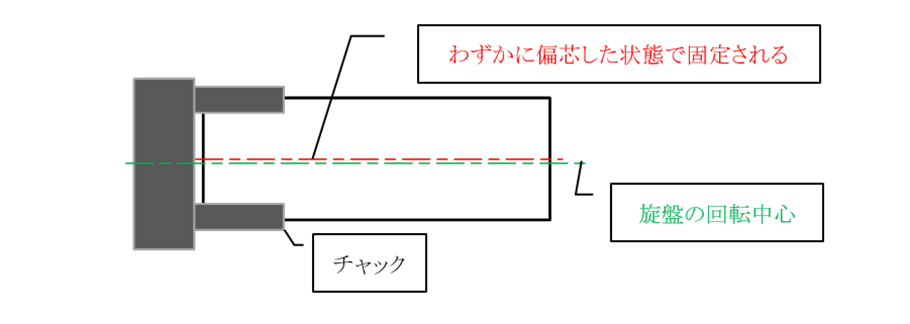
a) 丸棒をチャックで固定
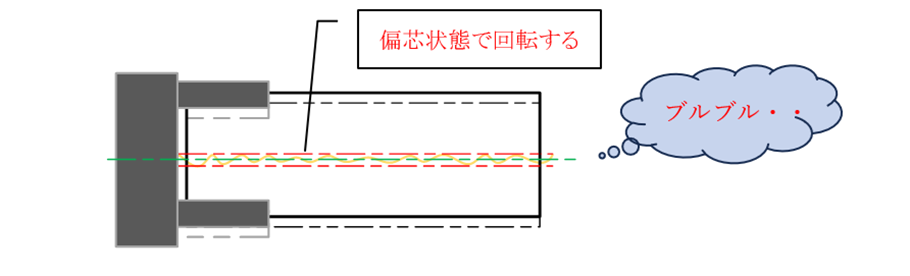
b-1) チャックごと芯ずれして回転する可能性
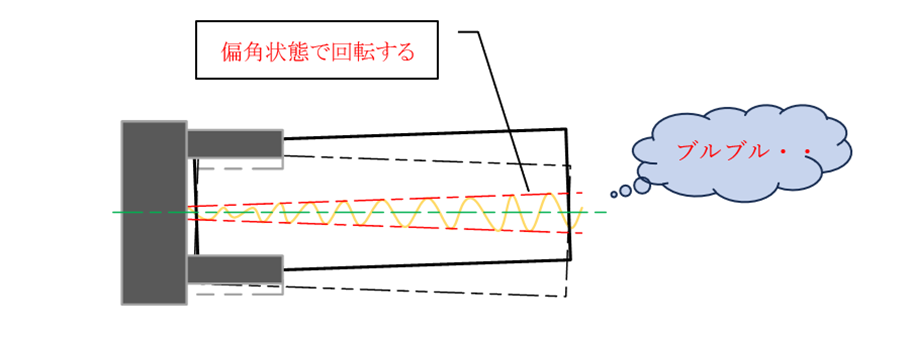
b-2) 素材が偏角して回転する可能性
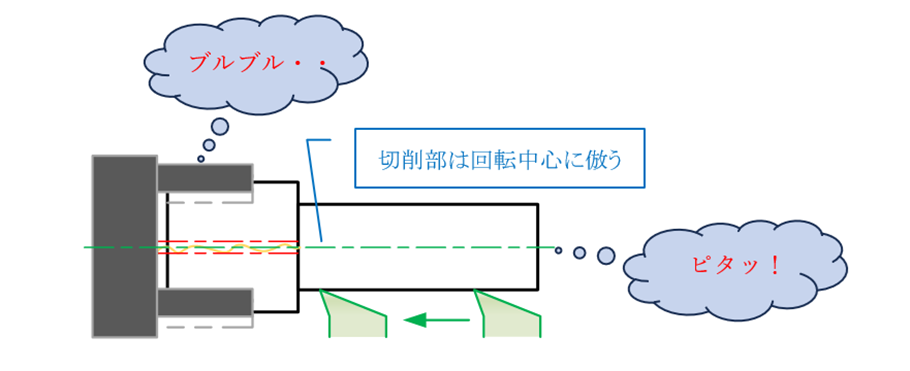
c) 切削部のみ旋盤の回転中心に倣(なら)う
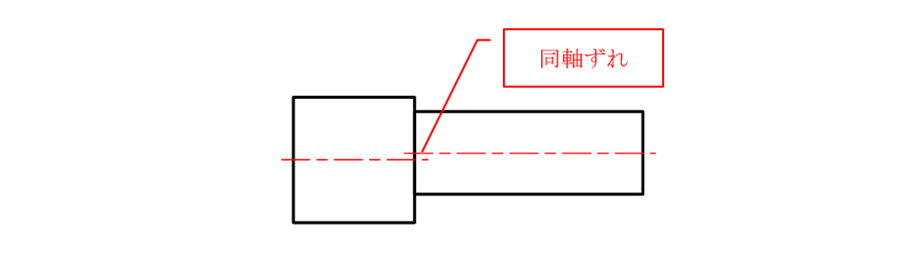
d) チャック固定部と切削円筒部の中心線がずれる
図15-3 同軸度が加工でずれる原理
4つ爪チャックの場合、材料をチャックした際に材料の中心線と旋盤の回転中心を合わせる目的でダイヤルゲージなどを使って芯ずれを補正します(図15-4)。

図15-4 ダイヤルゲージによる芯ずれの補正
6.同軸度/同心度の図面と公差領域
図面に同軸度/同心度を指示する場合の設計意図と図面指示例、公差領域を解説します。
① 台座に挿入する軸を基準とし、突出する側の軸に同軸度を指示する場合
設計意図
台座の穴に部品①の軸端部を挿入し、部品①の突出側の長い方の軸が台座の穴と同軸になるようにしたい(図15-5)。
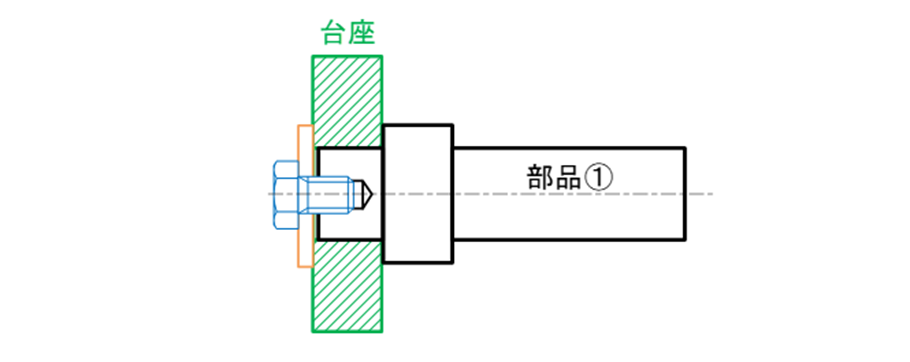
図15-5 部品①を台座の穴に対して同軸に取り付けたいという設計意図
図面指示
台座へ挿入する側の軸にデータムを付けて指示し、同軸にしたい長い方の軸に同軸度を指示します(図15-6)。
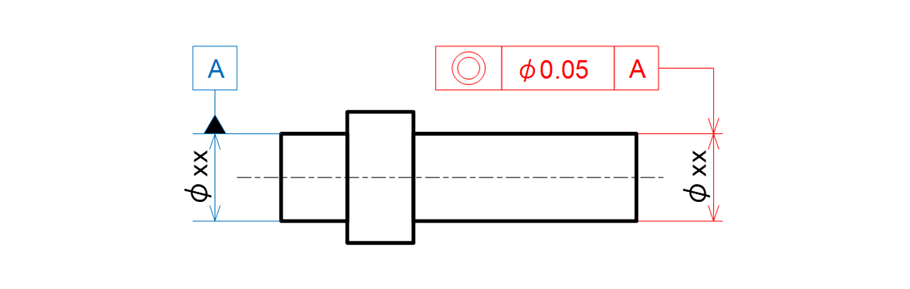
図15-6 同軸度を指示した例
公差領域
検査対象となる中心線は、データム中心線と同軸な直径0.05mmの円筒領域で規制されます(図15-7)。
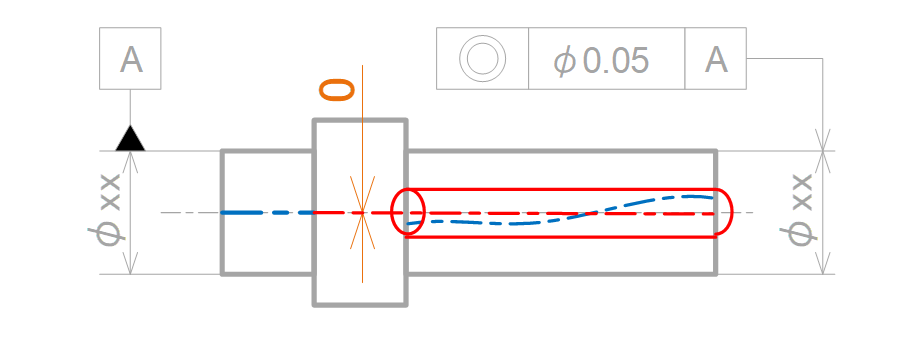
図15-7 同軸度を指示した時の公差領域
② 台座に挿入する軸を基準とし、突出する側の軸に同心度を指示する場合
設計意図
台座の穴に部品①の軸端部を挿入し、部品①の突出側の短い方の軸が台座の穴と同心になるようにしたい(図15-8)。
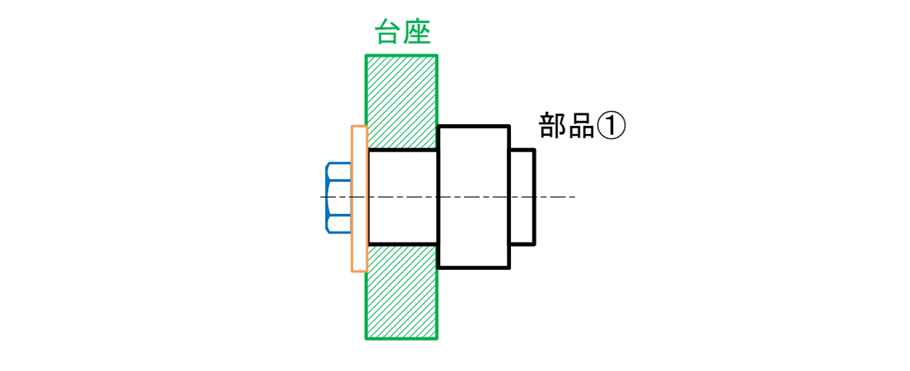
図15-8 部品①を台座の穴に対して同軸に取り付けたいという設計意図
図面指示
台座へ挿入する側の軸にデータムを付けて指示し、同心にしたい短い方の軸に同心度を指示します(図15-9)。
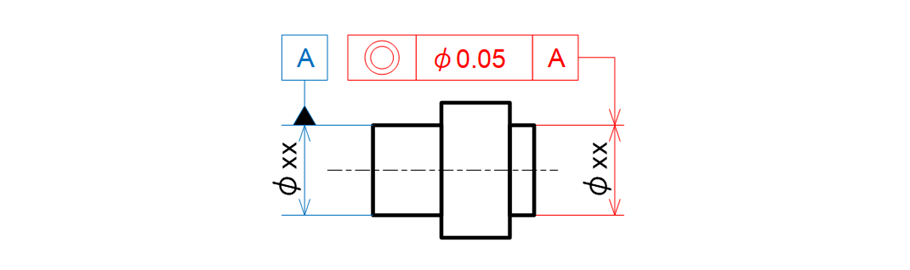
図15-9 同軸度を指示した例
公差領域(部品①)
検査対象となる中心線は、データム中心線と同心な直径0.05mmの円の領域で規制されます(図15-10)。
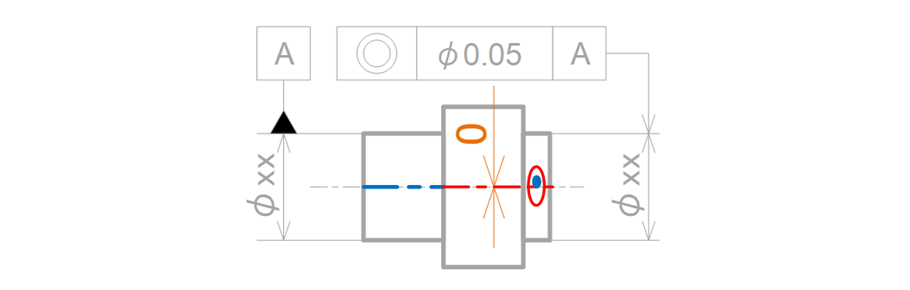
図15-10 同心度を指示した時の公差領域
③ 穴を基準に他方の穴に同軸度を指示する場合
設計意図
挿入する軸がスムーズに挿入できるよう部品①にある2つの穴が同軸であって欲しい(図15-11)。
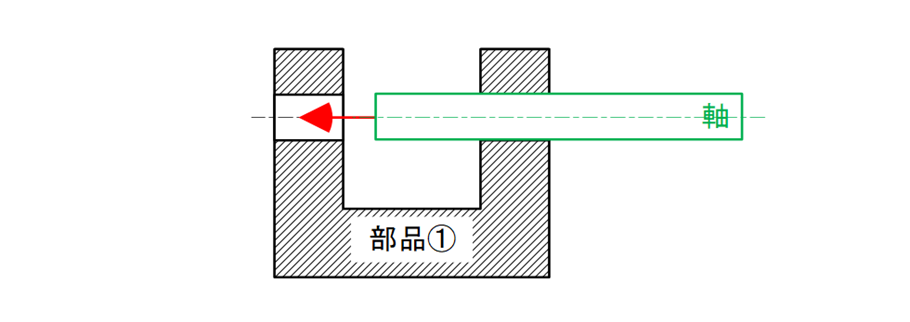
図15-11 2つの穴に軸をスムーズに挿入したい設計意図
図面指示
基準とする穴にデータムを付けて指示し、それと同軸になって欲しい穴に同軸度を指示します(図15-12)。
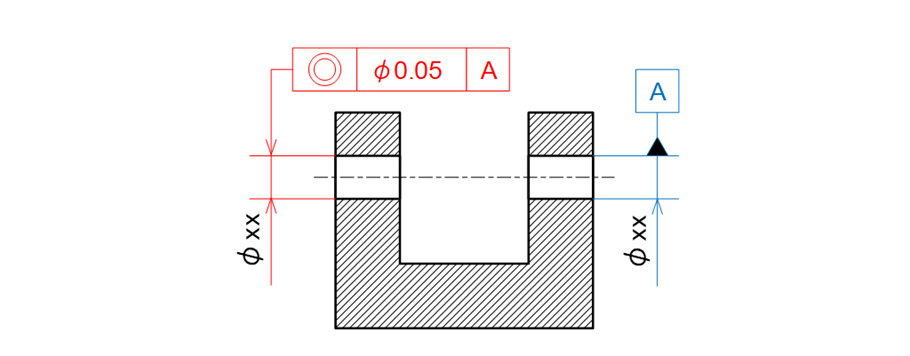
図15-12 穴の中心線を基準にして同軸度を他の穴の中心線に指示した例
公差領域
検査対象となる中心線は、データムの中心線と同軸な直径0.05mmの円筒領域で規制されます(図15-13)。
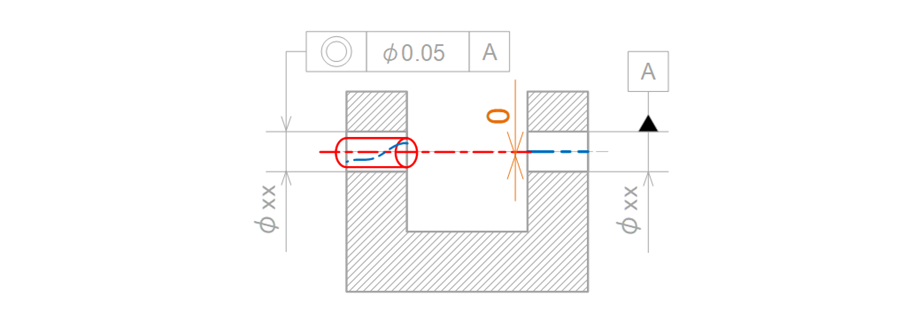
図15-13 穴の中心線を基準にして同軸度を他の穴の中心線に指示した時の公差領域
④ 穴を基準に他方の穴に同軸度を指示した場合の落とし穴
図15-12の例では、厚みがあることから切削部品をイメージすることができると思います。切削部品ですから穴の長さもそれなりにあることを前提としています。
同じような構造を板金で製作することができ、次のような図面も散見されます(図15-14)。
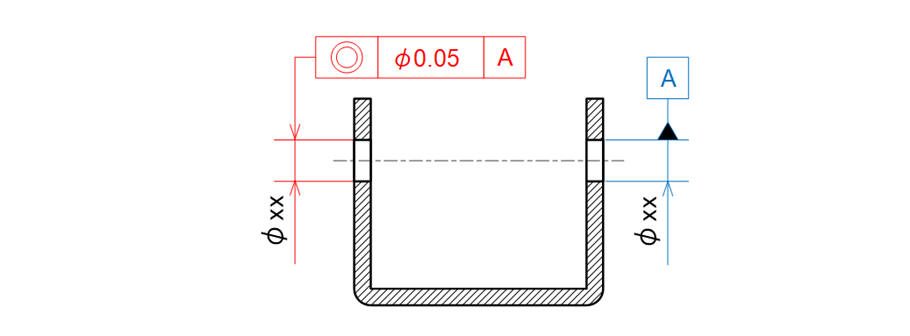
図15-14 コの字形の板金部品に同軸度を指示した例
しかし、厚みが1~2mm程度の薄板の場合、同軸度を検査することができないのです。
薄い板金穴を基準にすると基準が点になることで、同軸度が成り立たないのです。点は方向(ベクトル)をもたず、検査対象も点になることから穴位置がどこにずれていようが、2点間を直線で結ぶことができ同心度はゼロという結果なります(図15-15)。
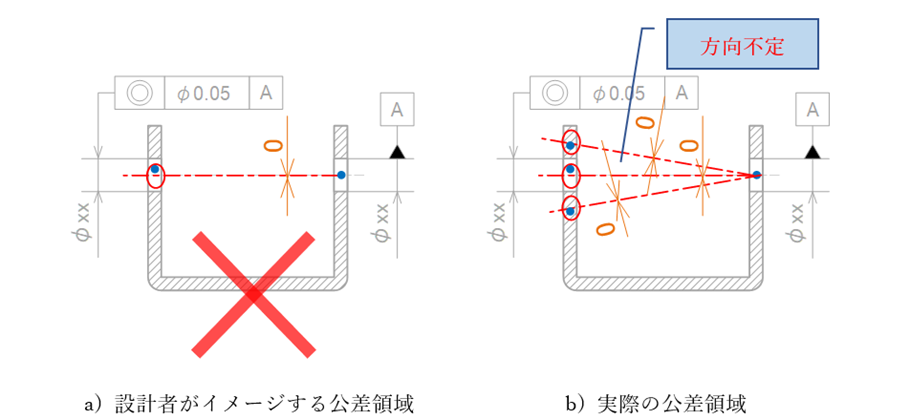
図15-15 同心度ゼロになる理由
それでは、コの字型の板金部品にはどのように指示するとよいのでしょうか?
共通領域(CZ)を利用した平行度と位置度の例を紹介します(図15-16)。
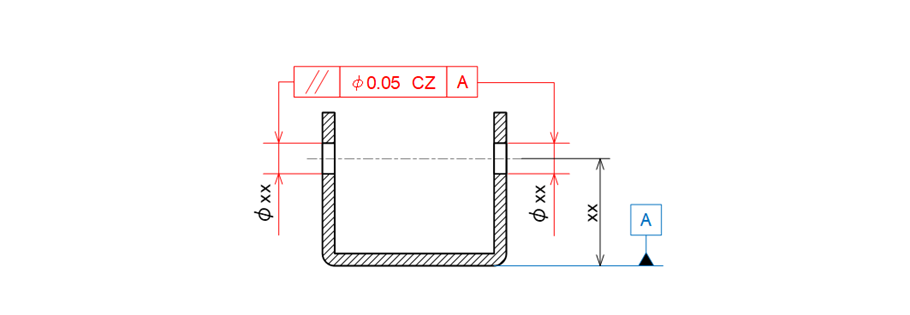
a) 2か所の穴を共通領域(CZ)にして平行度を使って指示する例(データム1つの例)
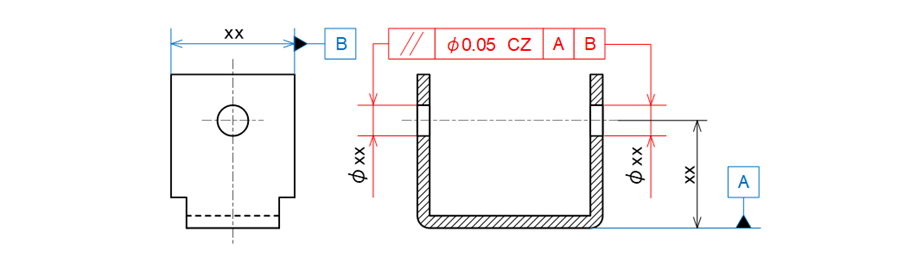
b) 2か所の穴を共通領域(CZ)にして平行度を使って指示する例(データム2つの例)
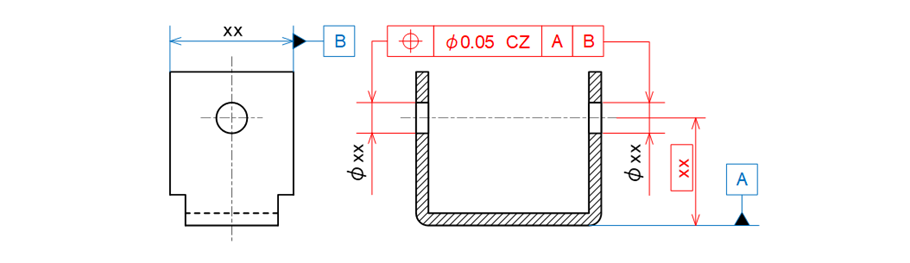
c) 2か所の穴を共通領域(CZ)にして位置度を使って指示する例(データム2つの例)
図15-16 コの字型の板金部品に平行度や位置度で指示して同心を表現した例
7.同軸度/同心度の検査方法
真円度測定機による同軸度の評価
真円度測定機は回転テーブルをもっているため同軸度が測定しやすい装置になります。
テーブルを回転させて、データム円筒部の2か所以上の円周線の情報を取得し2つ以上の中心点を合成してデータム中心線を認識させます。同様にテーブルを回転させて検査円筒部の2か所以上の円周線の情報を取得し、2つ以上の中心点を通る中心曲線を生成して同軸度を評価します(図15-17)
同軸度/同心度は、回転テーブルをもたないCNC3次元測定機で測定することもできます。
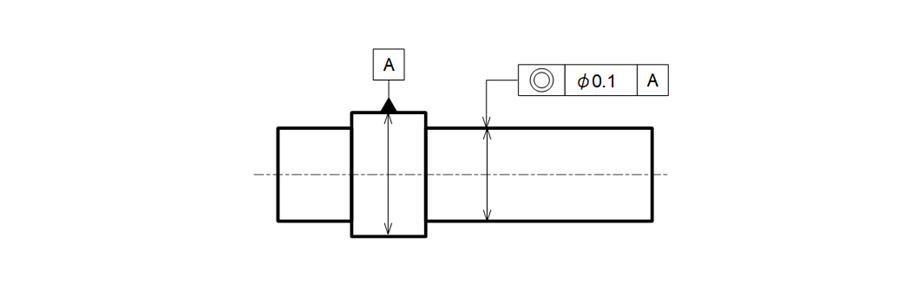
a) 図面指示例

図15-17 同軸度測定の例
まとめ
今回は、同軸度/同心度を指示する際のルールについて解説しました。
同じ記号を使用するにもかかわらず、検査対象が中心線の場合は同軸度、中心点の場合は同心度と呼び分けることも知りました。
肉厚の薄い板金部品などで同軸度が意味をなさないことも理解し、平行度や位置度を使うことで設計意図を表現できるテクニックも知りました。
同軸度/同心度は真円度測定機やCNC3次元測定機で測定することができます。
次回は、同軸度/同心度と同じ位置偏差のグループに属する対称度について解説します。



