基準と幾何特性は100年かけて図面を育てるんじゃ
今回のシリーズ記事は、グローバル図面に必須となる幾何公差の意味と図面のルールを解説します。第2回目のこの記事では、寸法公差と幾何公差の独立の原則と、包絡(ほうらく)の条件について解説します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >
目次
1.「公差」とは、部品における「ばらつき」の許容範囲を表すもの
部品におけるばらつきとは、「大きさの不揃い」と「形状の不揃い」に大別されます。
大きさの不揃いを許す範囲がサイズ公差(従来の寸法公差)で、カタチのばらつきを許す範囲が幾何公差で表されます。
そもそもサイズ公差があるのに、どうして幾何公差が必要なのでしょうか?
幾何公差を使わなくても問題が発生していないなら、「製図も面倒だし、わざわざコストアップになる幾何公差なんか使いたくない!」と考えている設計者も多いと思います。
しかし、幾何公差を使わなければ設計意図を図面に指示することができないのです。
1) 幾何公差の目的
サイズ公差は大きさを規制するだけのもので、形の崩れや狂い(反り・変形)に加えて位置ずれを心配しても規制することはできません。そこで、どの程度まで形や位置を正しく仕上げたらよいか、逆にいえば、どの程度までの形崩れや位置ずれであれば許されるのかが問題となり、それを数値化したものが幾何公差です。
2) サイズと幾何特性の関係
従来の寸法公差(現在はサイズ公差という)は“大きさ”を定義するのに対し、幾何公差は“カタチや姿勢、位置”を定義するため、それらを区別して図面に指示しなければいけません。
部品の個々の形体には次の4つの特性があります(図2-1)。
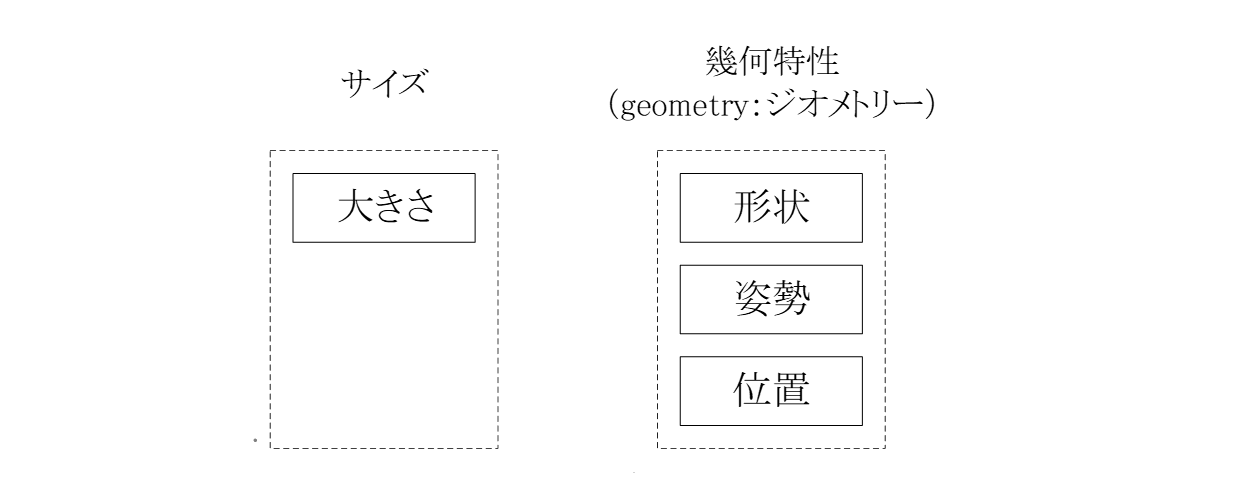
図2-1 大きさのばらつきとカタチのばらつき
設計意図を正しく図面に反映させるため、形状や姿勢、位置を幾何公差として図面に指示することをGD&T(Geometric Dimensioning & Tolerancing:幾何公差設計法)と呼びます。
広義の意味でGD&Tは、次の2点になります。
- 幾何公差を使って図面を描くこと。
- 公差計算によって累積する公差のばらつきを検討すること。
上記のどちらを優先すべきかという問題が生じますが、筆者は「幾何公差を使って図面を描くこと」によってばらつきの範囲を明確化した後に、「公差計算を行いばらつきの検討を行い、満足しない場合は公差の値や構造変更を実施する」ことで効率よく設計が進むと考えています。
2.独立の原則(JIS B 0024)とは
独立の原則とは、「図面に指示されたサイズ公差と幾何公差は、特別な相互関係が指定されない限り独立して別々に適用される」と定義されています。
つまりサイズ公差と幾何公差は互いに関連性はないという意味で、ISO(国際標準化機構)やJIS(日本産業規格)では独立の原則を採用しています。
1) 独立の原則
サイズとは長さ・幅・直径など実際の大きさを指し、サイズ公差(従来の寸法公差)で2点間距離のあるべき大きさからのばらつきを指示します。
幾何特性とは反り・角度ずれ・位置ずれなどを指し、幾何公差であるべき形状からの変化の度合いを指示します。
独立の原則の下では、サイズのばらつきとは別に形状ばらつき(変形)が加算されるため、軸の場合は最大外径を超える実効領域(物理的占有領域)を考える必要があります。
例えば、幾何公差の指示がなく軸径のサイズ公差が「0/-0.1」とだけ指定されている軸は、外径の任意の場所の測定ポイントでの値がφ9.9~φ10.0の範囲内であれば合格です。
しかし軸にα分の反りがあるとφ10.0+αの実効領域(物理的占有領域)が必要であることがわかります。ちなみにこのαの値はサイズ公差とは無関係に成り行きの変形量と考えます(図2-2)。
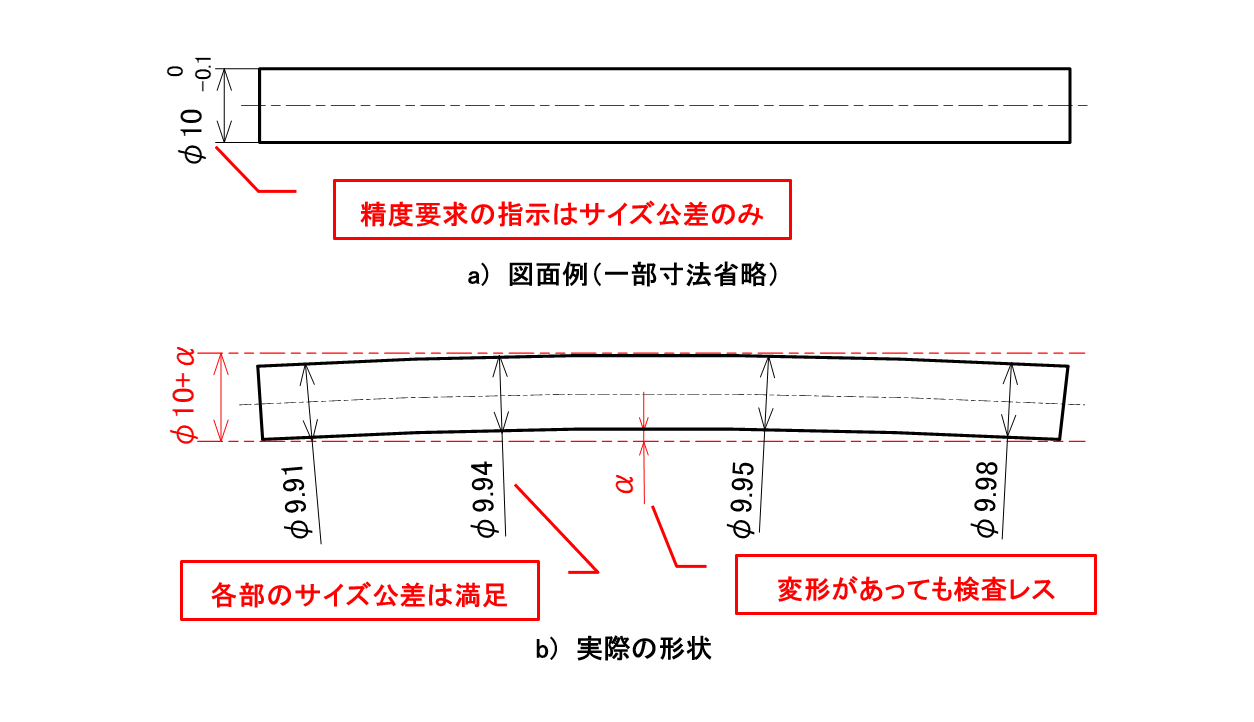
図2-2 サイズ公差の解釈(軸の場合)
同様に、幾何公差の指示がなく穴径のサイズ公差が「+0.1/0」とだけ指定されている穴は、内径の任意の場所の測定ポイントでの値がφ10.0~φ10.1の範囲内であれば合格です。
しかし穴にβ分の反りがあるとφ10.0-βの実効領域(物理的占有領域)が必要であることがわかります。ちなみにこのβの値はサイズ公差とは無関係に成り行きの変形量と考えます(図2-3)。
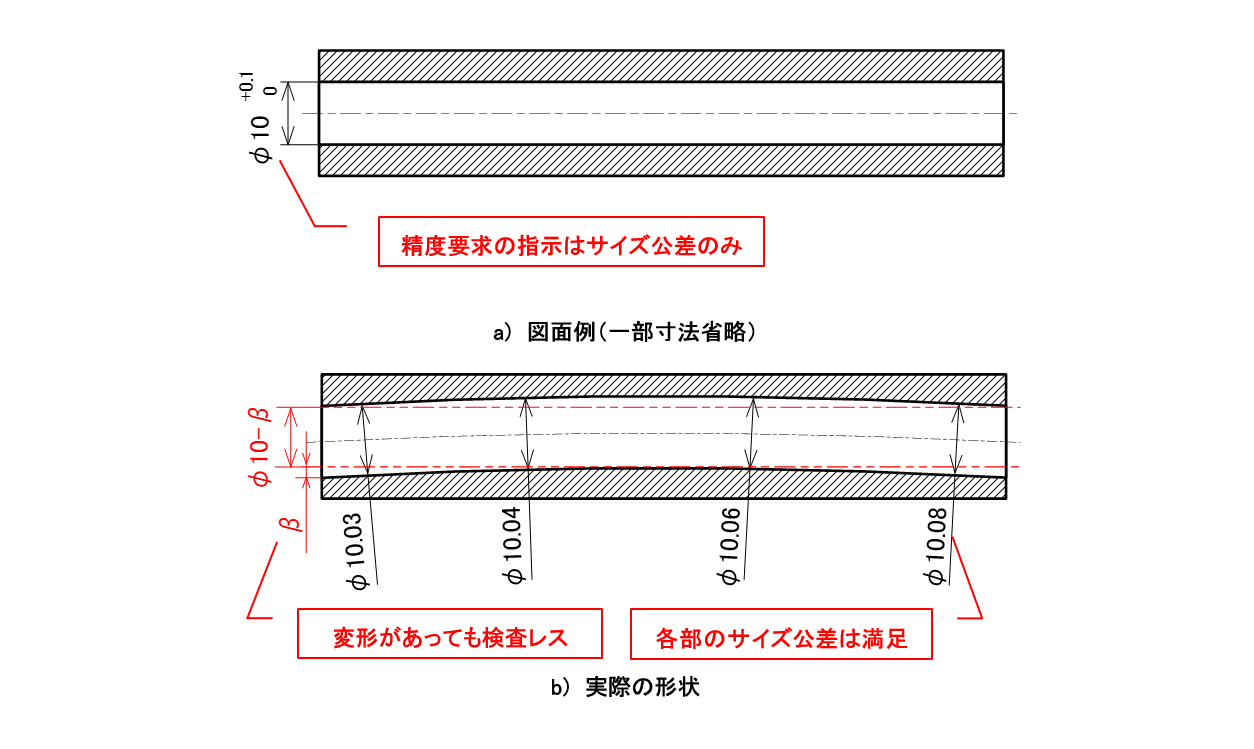
図2-3 サイズ公差の解釈(穴の場合)
このように、軸であろうと穴であろうと従来の寸法公差(サイズ公差)では、局部2点間距離を計測して合否を判断します。そのため軸や穴に反りがあっても、特に指示がなければ検査すらしてもらうことができずに合格品として納品されてしまうため、篏合する際に問題発生の可能性を秘めているのが独立の原則の特徴です。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >
3.包絡の条件(JIS B 0024)とは
包絡の条件とは、単独形体、つまり円筒面または平行二平面によって決められる一つの形体(サイズ形体)に対して適用し、形体がその最大実体寸法における完全形状の包絡面を超えてはならないことを意味します。
1) 包絡の条件の解釈
ここで、聞きなれないワード(最大実体寸法、完全形状の包絡面)が出てきましたのでそれらを説明します。
・最大実体寸法(MMR:Maximum Material Requirement)
形体のどこにおいても、その形体の実体が最大となるような許容限界寸法、たとえば最大の軸径、最小の穴径を持つ形体の寸法をいいます(図2-4)。
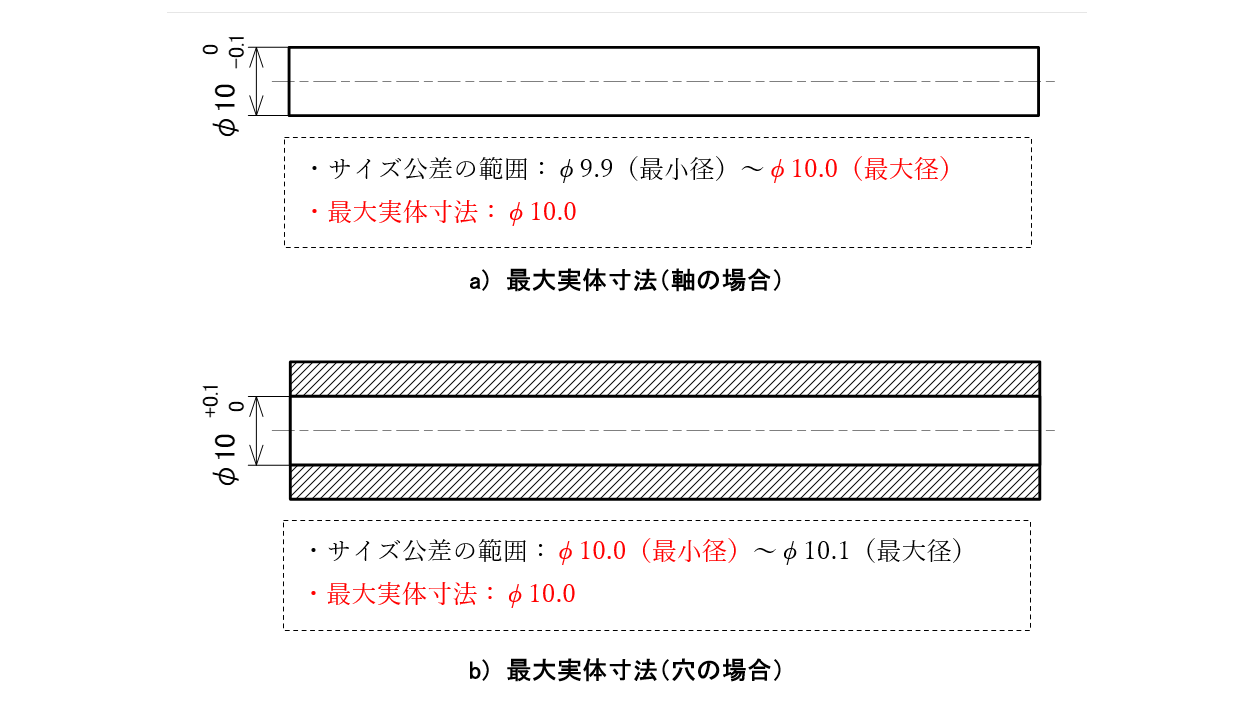
図2-4 最大実体寸法
・完全形状の包絡面
指示されたサイズ公差の最大実体寸法でできた形の崩れない領域のことを表わします。したがって、“完全形状の包絡面を超えてはならない”とは、カタチの崩れのない最大実体寸法の領域の中で、対象となる形体が存在しなければいけないということです。
図2-4 a)に示した軸の場合、最大実体寸法はφ10.0になり、この軸の完全形状の包絡面は曲がりのないφ10.0の円筒領域になります。
例えば軸径がたまたま最小径のφ9.9でできた場合、最大実体寸法φ10.0に対して0.1mmの差ができることになります。この差分を利用すれば、軸が最大0.1mm分反ったとしても包絡面を超えることはありません(図2-5)。
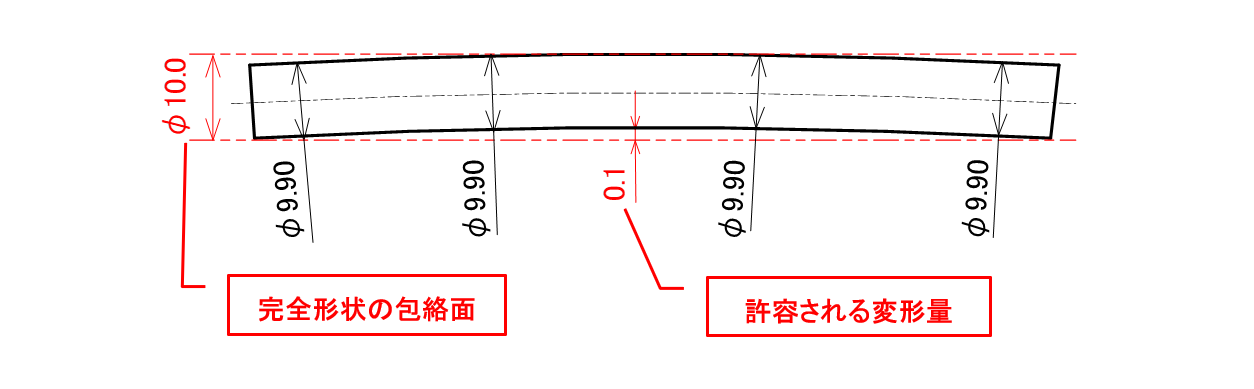
図2-5 包絡の条件における軸のサイズの関係
上記の例は、軸径がたまたま最小のφ9.9の時の変形量を表しています。
サイズ寸法は加工によってばらつきますから、軸径がφ9.91やφ9.95のように変化すると、それに合わせて変形したときの許される量が変動します。
軸径の成行き寸法ごとの許容される変形量の変化をまとめました(表2-1)。
表2-1 軸径の成行き寸法ごとの許容される変形量の変化
| 成行き寸法 | φ9.90 | φ9.91 | φ9.92 | φ9.93 | φ9.94 | φ9.95 |
| 許容変形量 | 0.10 | 0.09 | 0.08 | 0.07 | 0.06 | 0.05 |
| 成行き寸法 | φ9.96 | φ9.97 | φ9.98 | φ9.99 | φ10.00 | |
| 許容変形量 | 0.04 | 0.03 | 0.02 | 0.01 | 0.00 |
軸径がφ9.9の時は0.1mmの変形を許していましたが、軸径がφ9.9より太くなるに連れ、許容変形量が減り、最終的に成行き寸法がφ10.0の時には許容変形量が0.00となり、一切の変形を許さないことがわかります。
図2-4 b)に示した穴の場合、最大実体寸法はφ10.0になり、この穴の完全形状の包絡面は曲がりのないφ10.0の円筒領域になります。
例えば、穴径がたまたまφ10.1でできた場合、最大実体寸法φ10.0に対して0.1mmの差ができることになります。この差分を利用すれば、穴が最大0.1mm分反ったとしても包絡面を超えることはありません(図2-6)。
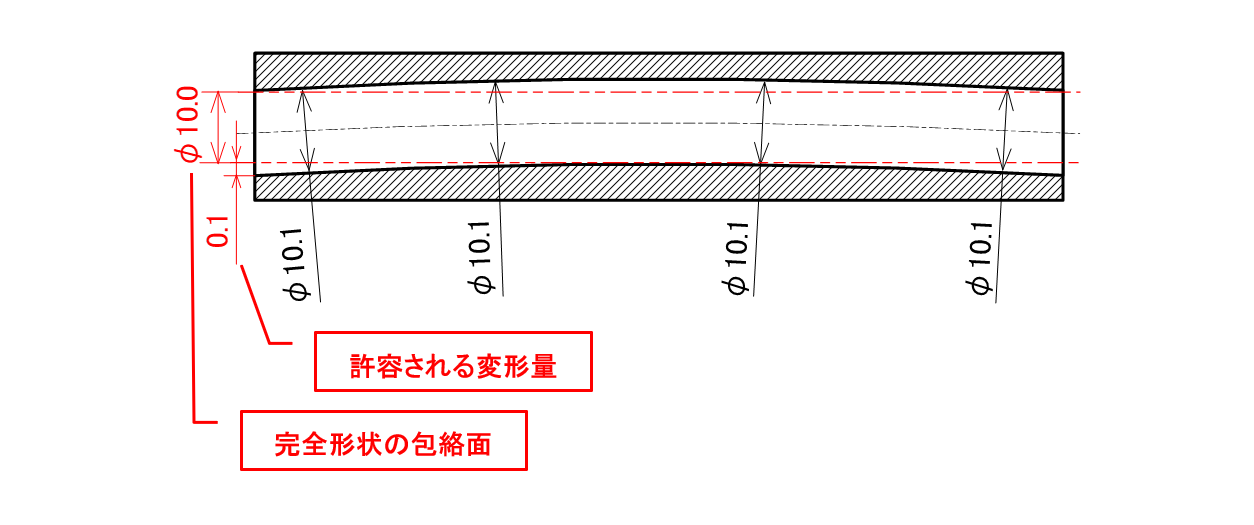
図2-6 包絡の条件における穴のサイズの関係
上記の例は、穴径がたまたま最大のφ10.1の時の変形量を表しています。
サイズ寸法は加工によってばらつきますから、穴径がφ10.05やφ10.01のように変化すると、それに合わせて変形しても許される量が変動します。
穴径の成行き寸法ごとの許容される変形量の変化をまとめました(表2-2)。
表2-2 穴径の成行き寸法ごとの許容される変形量の変化
| 成行き寸法 | φ10.1 | φ10.09 | φ10.08 | φ10.07 | φ10.06 | φ10.05 |
| 許容変形量 | 0.10 | 0.09 | 0.08 | 0.07 | 0.06 | 0.05 |
| 成行き寸法 | φ10.04 | φ10.03 | φ10.02 | φ10.01 | φ10.00 | |
| 許容変形量 | 0.04 | 0.03 | 0.02 | 0.01 | 0.00 |
穴径がφ10.1の時は0.1mmの変形を許していましたが、穴径がφ10.1より小さくなるに連れ、許容変形量が減り、最終的に成行き寸法がφ10.0の時には許容変形量が0.00となり、一切の変形を許さないことがわかります。
4.JIS(日本産業規格)製図の下で包絡の条件を適用する手段
JIS規格やISO規格は、特に明記しない限り独立の原則を適用しています。
独立の条件の下で描いた図面の中で、一部分だけ包絡の条件を使いたい場合は、個別のサイズ寸法の後に丸で囲んだEの記号を付記します(図2-7)。
Eは、「Envelope(=封筒)」の頭文字をとったもので、完全形状の包絡面が封筒を意味していると考えるとよいでしょう。
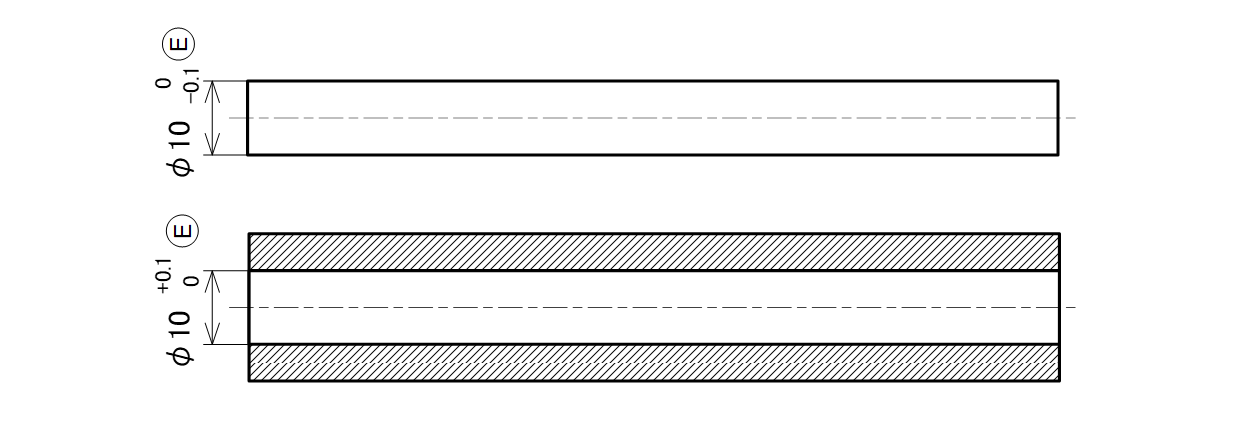
図2-7 包絡の条件を指定した記入法の例
一部に包絡の条件を適用するのではなく図面全てに包絡の条件を適用する場合は、表題欄やその付近に包絡の条件を規定している規格を明記しなければいけません。
世界標準(ISO規格)である独立の原則と違った解釈をするものに、アメリカ機械学会の規格にASME Y14.5M(Dimensioning and Tolerancing)があります。
このASME Y14.5Mでは独立の原則を適用せず、最初から包絡の条件が適用されます。
したがって、図中に「本図はASME Y14.5Mに順ずる」など注記を書く必要があります。
まとめ
今回は、従来の寸法公差(サイズ公差)と幾何公差の違いを独立の原則と包絡の条件を用いて紹介しました。
サイズ公差は局部の2点間距離を測定するため、全体が反っているなど俯瞰して状態を見ることができません。そのため幾何公差の指示がなければ、明らかに異常な変形でない限り検査を素通りしてしまうことがわかりました。
包絡の条件を一部のサイズに適用するテクニックも知りました。多くの日本人技術者は、この包絡の条件を知りません。しかし変形が予想される形体(長い軸や長い穴など)のはめあいには、互いに篏合する部分のサイズ公差に丸で囲んだEの記号を記入する方が設計意図をより明確に表現できると考えます。
次回は、検査をする際に姿勢を決める役割を果たすデータムを解説します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >






