グローバル図面として設計意図を表す幾何公差の意味
今回のシリーズでは、グローバル図面に必須となる幾何公差の意味と図面のルールを解説します。第4回目のこの記事では、幾何特性14種類とその使い方を詳しく説明します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >
目次
1.幾何公差の基本概念(JIS B 0021)
JISで規定されている幾何公差の基本概念を以下に示します。
①形体に指示した幾何公差は、その中に形体が含まれる公差域を定義する。
②形体とは、表面、穴、溝、ねじ山、面取り部分または輪郭のような加工物の特定の特性の部分であり、これらの形体は、現実に存在しているもの(例えば、円筒の外側表面)または派生したもの(例えば、軸線または中心平面)である。
③公差が指示された公差特性とサイズの指示方法によって、公差域は次のひとつになる。
- 円の内部の領域
- 二つの同心の円の間の領域
- 二つの等間隔の線または平行二直線の間の領域
- 円筒内部の領域
- 同軸の二つの円筒の間の領域
- 二つの等間隔の表面または平行二平面の間の領域
- 球の内部の領域
④更に限定した公差が要求される場合、例えば注記を除いて、公差付き形体はこの公差領域内で任意の形状または姿勢でもよい。
⑤特に指示した場合を除いて、公差は対象とする形体の全域に適用する。
⑥データムに関連した形体に指示した幾何公差は、データム形体自身の形状偏差を規制しない。データム形体に対して、形状偏差を指示してもよい。
設計者はCAD上に直線や平面、円や円筒、あるいは曲線や曲面を描いて設計を進めていきます。組立図であろうと部品図であろうと、そこには大きさのばらつきがなく、形の崩れや位置ずれのない完全状態の形状が図示されています。つまり図面は“絵に描いた餅”であるのです。
1) 幾何公差の目的
加工者は図面を見てできるだけ忠実に正しい直線、円あるいは平面に加工しようとしますが、完全に正しい大きさ(ばらつきのない直径や長さなど)や完全に正しい形状(幾何学的に正しい直線、円、平面など)に仕上げることは不可能です。
完全に正しい形状からずれてしまう問題に完全なよりどころを与えるために対象物の形状や姿勢、位置の狂い(これらを幾何偏差という)に明確な定義を与え、その幾何偏差の許容値(幾何公差という)の表示並びに図示法について定めたものが幾何公差です。
つまり、あるべき幾何学的な形状からどの程度までの狂いであれば許されるのを規定するもので、サイズ公差(従来の寸法公差)だけでは表しきれないものを補完するものです。
2) 14種もある幾何特性
JISに定められた幾何特性の種類は、全部で14種類あります。幾何公差の最初のステップは、14種類の幾何特性の名称と記号を覚えることです。特に幾何特性の記号を暗記するのは難しく思うかもしれませんが、視覚的に目的とする特性に似た記号が用いられていますので心配することはありません(表4-1)。
表4-1 幾何特性記号の表す意味
| 名称 | 記号 | 意味 |
| 真直度 |  |
理論的に正確な直線からどれだけ変形しているかを表す |
| 平面度 |  |
理論的に正確な平面からどれだけ変形しているかを表す |
| 真円度 |  |
理論的に正確な真円からどれだけ変形しているかを表す |
| 円筒度 |  |
理論的に正確な円筒からどれだけ変形しているかを表す |
| 線の輪郭度 |  |
理論的に正しい母線形状からどれだけ変形しているかを表す |
| 面の輪郭度 | 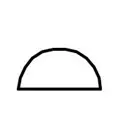 |
理論的に正しい表面形状からどれだけ変形しているかを表す |
| 平行度 |  |
基準に対してどれだけ平行から傾いているかを表す |
| 直角度 | 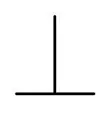 |
基準に対してどれだけ直角から傾いているかを表す |
| 傾斜度 | 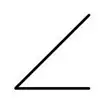 |
基準に対してどれだけ理論的に正確な角度から傾いているかを表す |
| 同軸度
同心度 |
 |
基準に対して中心線がどれだけ位置ずれしているかを表す
基準に対して中心点がどれだけ位置ずれしているかを表す |
| 対称度 | 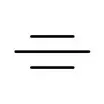 |
基準に対して中心平面がどれだけ位置ずれしているかを表す |
| 位置度 | 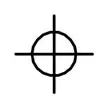 |
基準に対してあるべき位置に対してどれだけ位置ずれしているかを表す |
| 円周振れ |  |
基準線を中心に回転させたとき、任意の位置の母線がどれだけ振れているかを表す |
| 全振れ |  |
基準線を中心に回転させたとき、表面全体がどれだけ振れているかを表す |
これら14種類の特性は、次に示す4つの偏差に分類することができます(表4-2)。
表4-2 幾何特性の分類
| 偏差の名称 | データム | 幾何偏差 | |
| 形状偏差 | 単独形体 | 不要 | 真直度・平面度・真円度・円筒度・線の輪郭度・面の輪郭度 |
| 姿勢偏差 | 関連形体 | 要(*) | 平行度・直角度・傾斜度・線の輪郭度・面の輪郭度 |
| 位置偏差 | 同軸/同心度・対称度・位置度・線の輪郭度・面の輪郭度 | ||
| 振れ偏差 | 円周振れ・全振れ | ||
*位置度はデータム無しで使用することもできます。
表4-2より、線の輪郭度と面の輪郭度は形状偏差、姿勢偏差、位置偏差と重複していることから他の特性と比べて自由度の高い特性であることがわかります。
2. 公差記入枠の記入法
幾何公差を図面に表現するためには、公差記入枠という長方形のフレーム内に幾何特性記号や幾何公差値、その他の記号、データムを記入します。公差記入枠は水平に配置した2つまたはそれ以上に分割した長方形の枠に指示線をつけて表します。指示線は公差記入枠の左右どちらから引き出しても構いません(図4-1)。
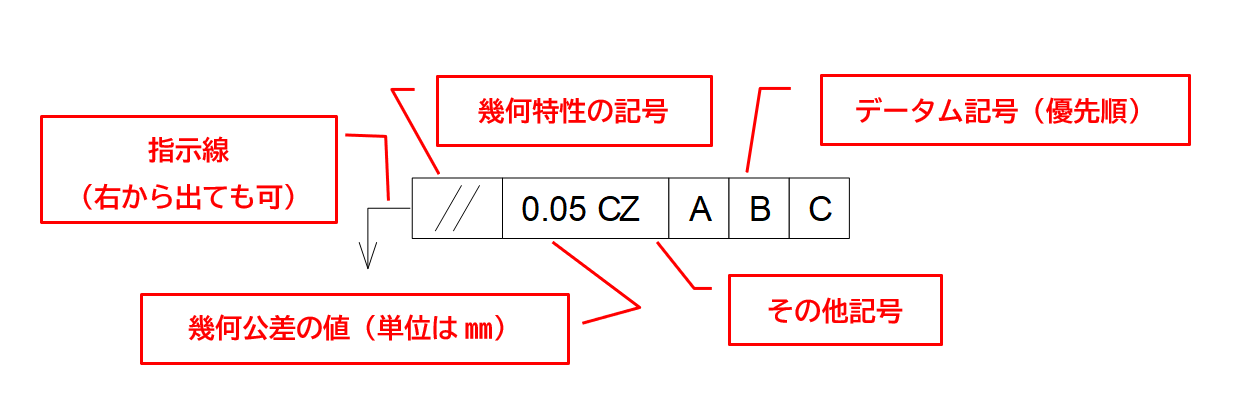
図4-1 公差記入枠の記入例
データムは貼り付ける場所で表面形体か中心形体(誘導形体とも呼ぶ)に分かれると前回の記事で解説しました。同様に公差記入枠から引き出す指示線についても指示する場所で表面形体か中心形体(誘導形体とも呼ぶ)に分かれます。
寸法線から明確に外して公差記入枠から引き出した指示線を付けた場合、幾何公差は表面あるいは母線が検査対象の形体であることを意味します(図4-2)。
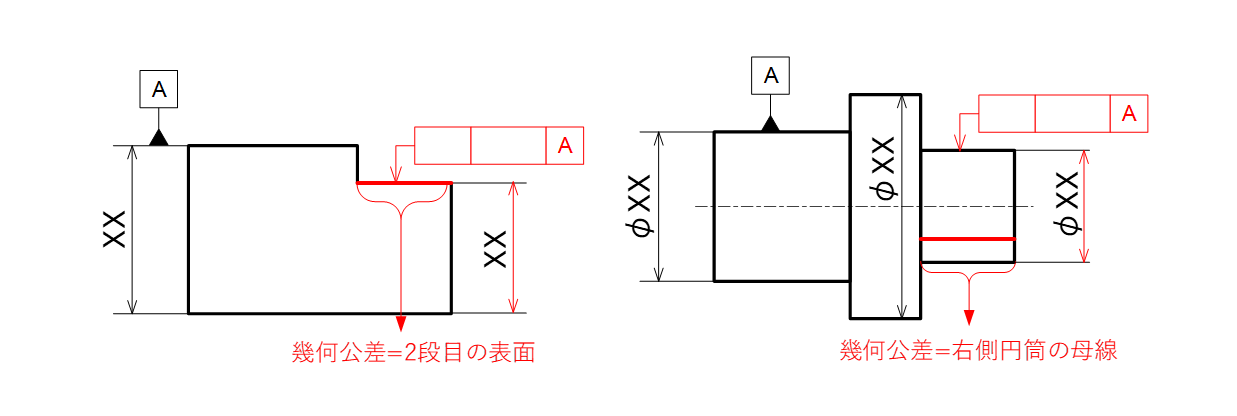
図4-2 表面あるいは母線への幾何公差指示
寸法線の延長線上に公差記入枠から引き出した指示線を付けた場合、幾何公差は中心点あるいは中心線、中心平面が検査対象の形体であることを意味します(図4-3)。
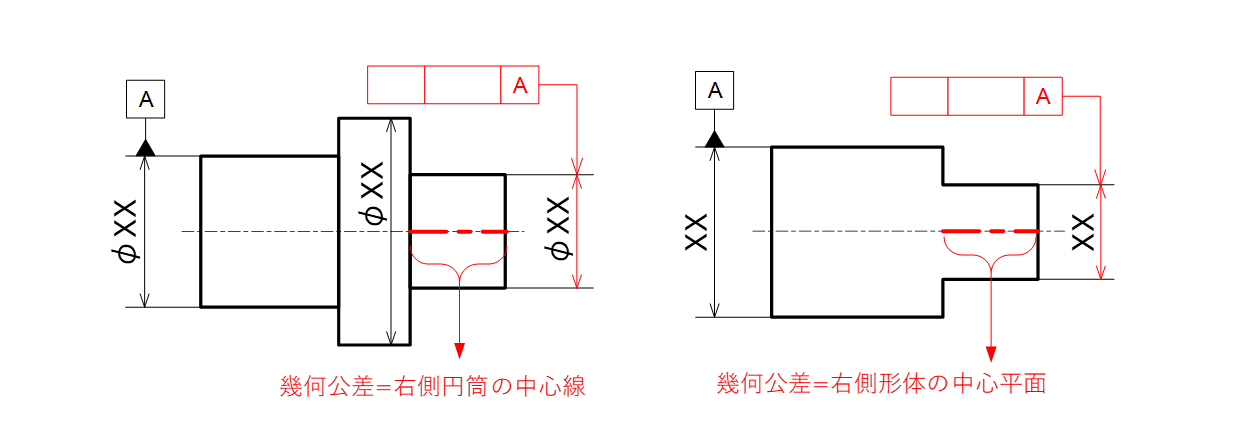
図4-3 中心線あるいは中心平面への幾何公差指示
3.公差記入枠の周辺に付与する記号たち
設計意図をより明確にするため、記入枠の周辺に様々な記号を付与することができます。その中でもよく使う記号を紹介します。
1) 複数の形体を包括した1つの形体とみなす記号
同一平面上、あるいは同一円筒面上に設計された複数の分離した形体を1つの形体とみなして幾何公差を適用する場合、公差記入枠内の幾何公差の値に続けて記号「CZ」を記入します。記号CZは、「Common Zone(共通領域)」の略になります(図4-4)。
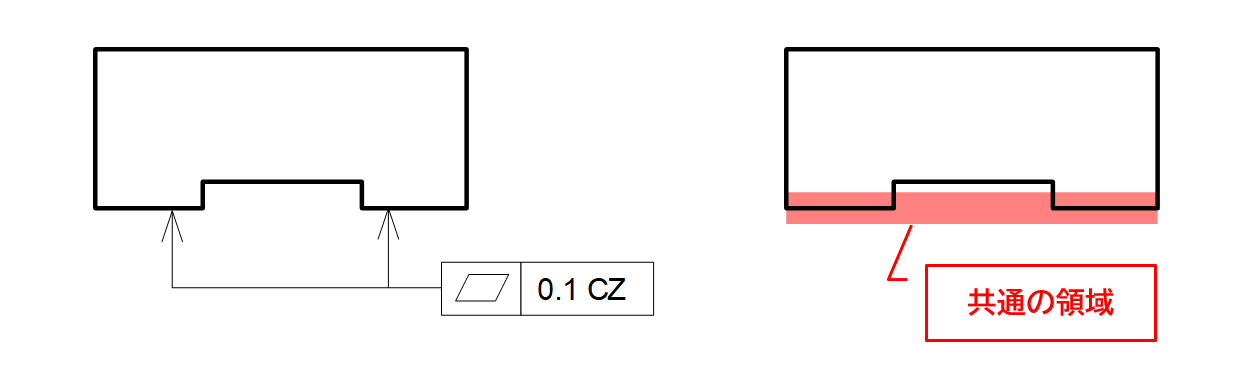
図4-4 共通領域を示す記号
2) 幾何公差の適用領域を指定する記号
幾何公差は指示線の矢を当てた形体のみに適用し、その形体が終了する箇所が境界位置となります。この境界を越えて複数の形体にまで幾何公差を適用する場合は、適用する区間がわかるようにアルファベットと両向き矢印で指示することができます(図4-5)。
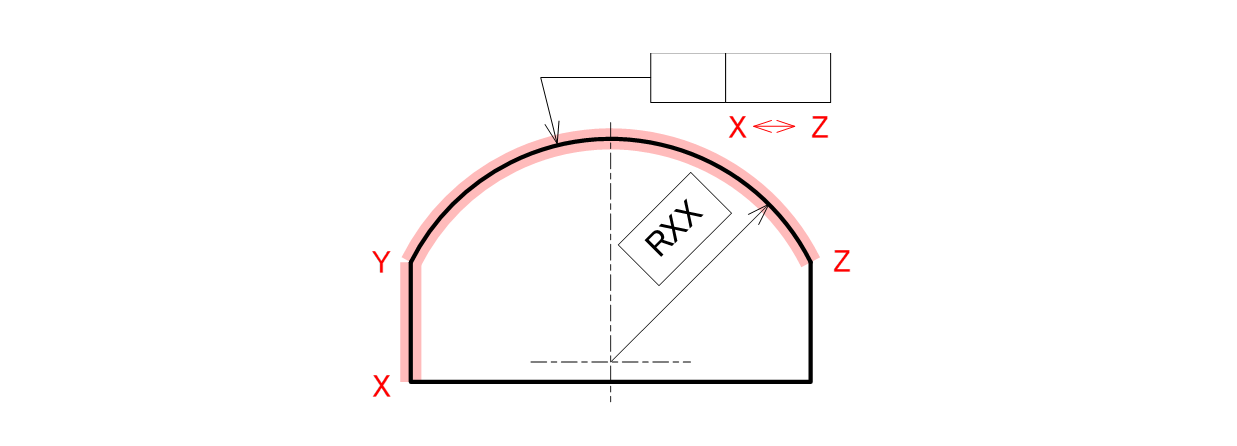
図4-5 限定した部分に公差を指示する記入例
3) 複数の形体に同時に幾何公差を指示する場合
幾何公差を2つ以上の形体に適用する場合、公差記入枠の上側にその数を表す値とサイズの間に記号〝×〟を用いて形体の数を指示します。サイズがない表面形体には個数と記号〝×〟のみを記入します(図4-6)。
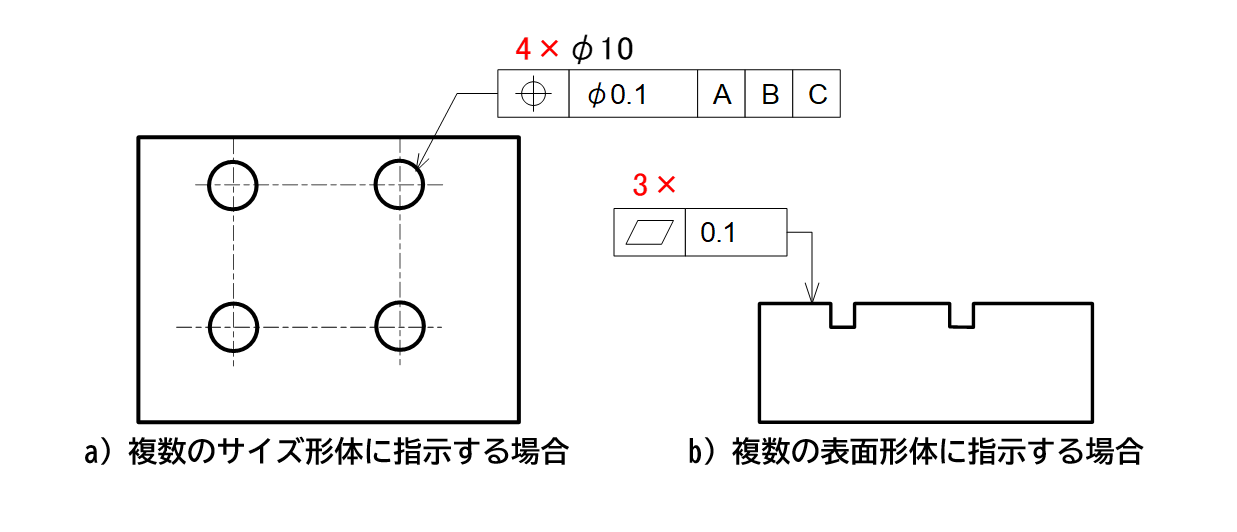
図4-6 複数形体に幾何公差を指示する記入例
4) 形体全周に幾何公差を指示する場合
輪郭度などを表面形体の全周に幾何特性を適用する場合には、〝全周〟を表す記号「○」を指示線の角部に付与します(図4-7)。
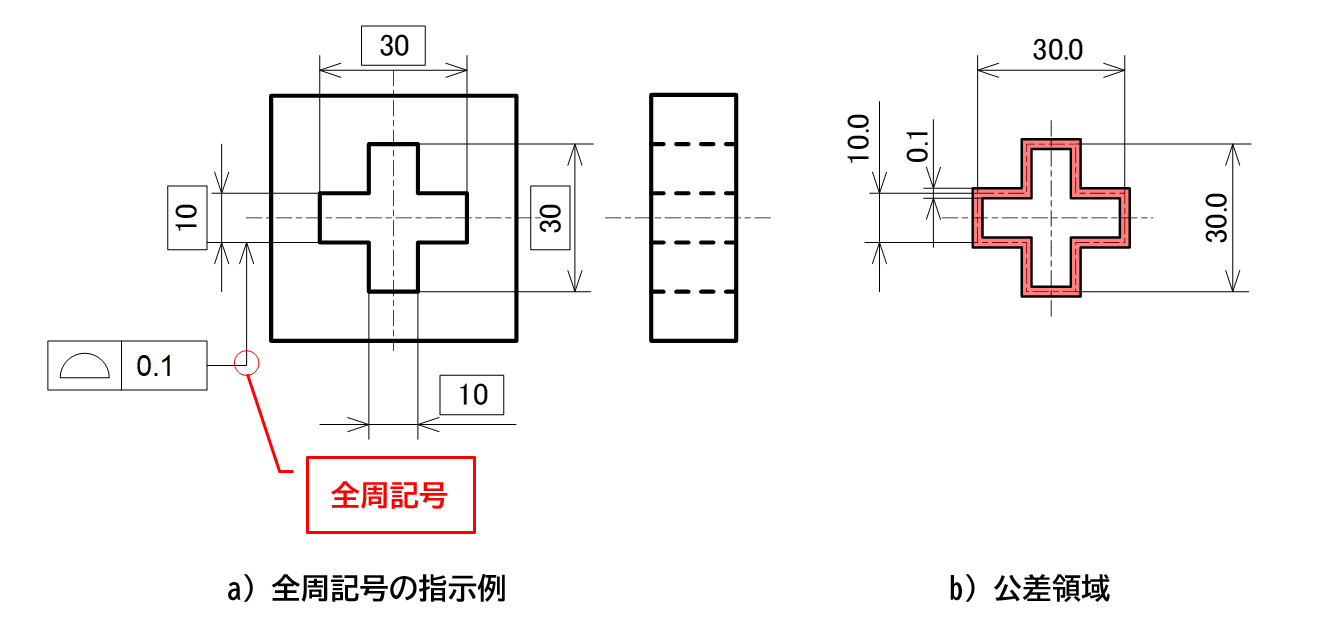
図4-7 全周に幾何公差を指示する記入例
4. 普通幾何公差
サイズの普通許容差(普通公差や一般公差とも呼ぶ)と同じく、幾何公差にも普通許容差の規定があります。普通幾何公差はJIS B 0419に規定され、主として機械加工される形体に適用されます。板金曲げの普通幾何公差については、ベンディングマシンのメーカから一般的な情報をもらうとよいでしょう。
普通幾何公差の考え方は、「サイズの普通許容差」と同様に、個々の工場で通常得られる加工精度を考慮し等級を決定します。
幾何特性14種類ののうち7種類のみ普通幾何公差が適用されます(表4-3)。
表4-3 普通幾何公差の適用
| 幾何特性 | 普通幾何公差の適用 | 幾何特性 | 普通幾何公差の適用 |
| 真直度 | ○ | 直角度 | ○ |
| 平面度 | ○ | 傾斜度 | × |
| 真円度 | ○ ※1 | 同軸/同心度 | × |
| 円筒度 | × | 対称度 | ○ |
| 線の輪郭度 | × | 位置度 | × |
| 面の輪郭度 | × | 円周振れ | ○ |
| 平行度 | ○ ※2 | 全振れ | × |
※1 真円度は、直径のサイズ公差に等しくとるが、円周振れの公差を超えてはならない
※2 平行度は、サイズ公差と平面度公差・真直度公差のいずれか大きいほうの値をとる
普通幾何公差の公差等級には、H,K,Lの3種類があり、選定する場合は個々の工場で通常に得られる加工精度が考慮されます(表4-4~表4-7)。
表4-4 真直度及び平面度の普通公差
|
公差 |
呼び長さの区分 | |||||
| 10以下 | 10より上 30以下 |
30より上 100以下 |
100より上 300以下 |
300より上 1000以下 |
1000より上 3000以下 |
|
| 真直度公差及び平面度公差 | ||||||
| H | 0.02 | 0.05 | 0.1 | 0.2 | 0.3 | 0.4 |
| K | 0.05 | 0.1 | 0.2 | 0.4 | 0.6 | 0.8 |
| L | 0.1 | 0.2 | 0.4 | 0.8 | 1.2 | 1.6 |
表4-5 直角度の普通公差
| 公差等級 | 短い方の辺の呼び長さの区分 | |||
| 100以下 | 100より上 300以下 |
300より上 1000以下 |
1000より上 3000以下 |
|
| 直角度公差 | ||||
| H | 0.2 | 0.3 | 0.4 | 0.5 |
| K | 0.4 | 0.6 | 0.8 | 1 |
| L | 0.6 | 1 | 1.5 | 2 |
表4-6 対称度の普通公差
| 公差等級 | 呼びの長さの区分 | |||
| 100以下 | 100より上 300以下 |
300より上 1000以下 |
1000より上 3000以下 |
|
| 対称度公差 | ||||
| H | 0.5 | |||
| K | 0.6 | 0.8 | 1 | |
| L | 0.6 | 1 | 1.5 | 2 |
表4-7 円周振れの普通公差
| 公差等級 | 円周振れ |
| H | 0.1 |
| K | 0.2 |
| L | 0.3 |
普通幾何公差を普通サイズ公差とともに適用する場合は、普通公差として表題欄の中、またはその付近に明記します(図4-8)。
例)機械加工において、普通サイズ公差がJIS B 0405の中級(記号m)で、かつ普通幾何公差はJIS B 0419の公差等級Kとする場合。
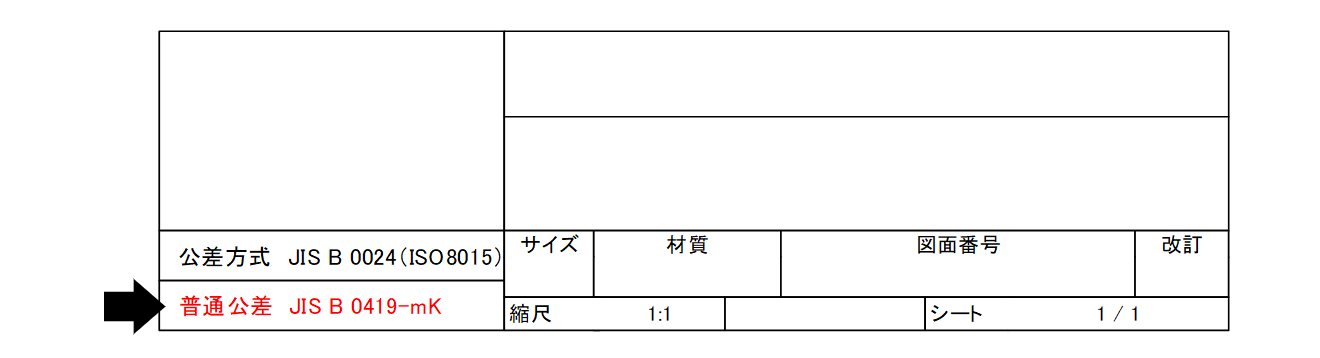
図4-8 表題欄内に表示した普通公差
「JIS B 0419-mK」は下記の2つの規格を合体したものです(図4-9)。

図4-9 普通公差指示の意味
まとめ
今回は、幾何公差を表現するための特性の種類と、それらを表現する公差記入枠について解説しました。
データムの図示方法と同様に公差記入枠から引き出す指示線を当てる場所によって、表面形体か中心形体に分かれることを知りました。
公差記入枠の内部、あるいは外部に指示する記号を活用することで様々な設計意図を表現できることも分かったと思います。
次回は、14種類ある幾何特性のうち、形状偏差の真直度について解説します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >




