真円度の記号は「〇(真ん丸な円!)」と覚える
今回のシリーズでは、グローバル図面に必須となる幾何公差の意味と図面のルールを解説します。第7回目のこの記事では、真円度の意味と記号の使い方を詳しく説明します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >
目次
1.形状偏差とは
前回の記事に続いて、14種類ある幾何特性の詳細について解説していきます。今回は、形状偏差というグループに含まれる真円度です。
形状偏差は単独形体に分類され、データムに関連がなく、幾何偏差が決められる形体になります。
形状偏差には次の6つの幾何特性があります。
・真直度
・平面度
・真円度 ←今回解説する幾何特性
・円筒度
・線の輪郭度…形状偏差の場合、データムに関連しない
・面の輪郭度…形状偏差の場合、データムに関連しない
2.真円度とは(JIS B 0682-1:2017)
真円度は「円形形体の幾何学的に正しい円からの狂いの大きさ」とJISで規定されます。真円度は形状偏差のグループに属するためデータムを必要としませんが、データムの代わりに“基準円(真円度曲線に当てはめた円)”を利用します。
基準円と真円度曲線(実際の円)の最大値(外側)および最小値(内側)に接し、間隔が最小になる二つの同心円間を測定します(図7-1)。
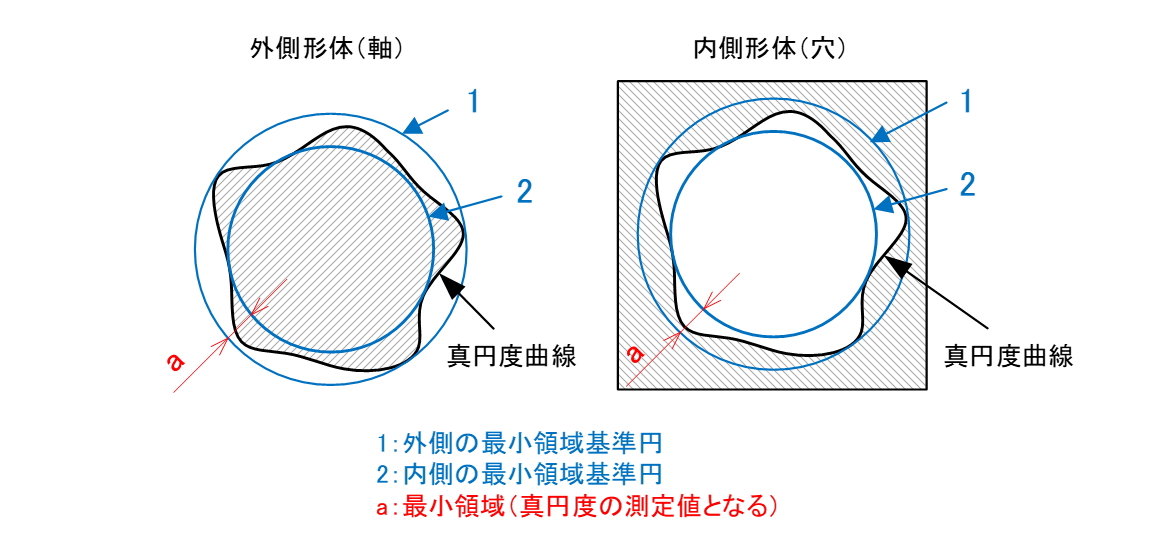
図7-1 真円度曲線と最小領域基準円の偏差
3. 真円度の記号と記入のルール
真円度を図面に表現する場合、公差記入枠に真円度の記号と幾何公差値、必要に応じてその他の記号を記入します。公差記入枠は2つの区画のものを使い、データムを記入する左から3番目以降の区画は存在しません(図7-2)。
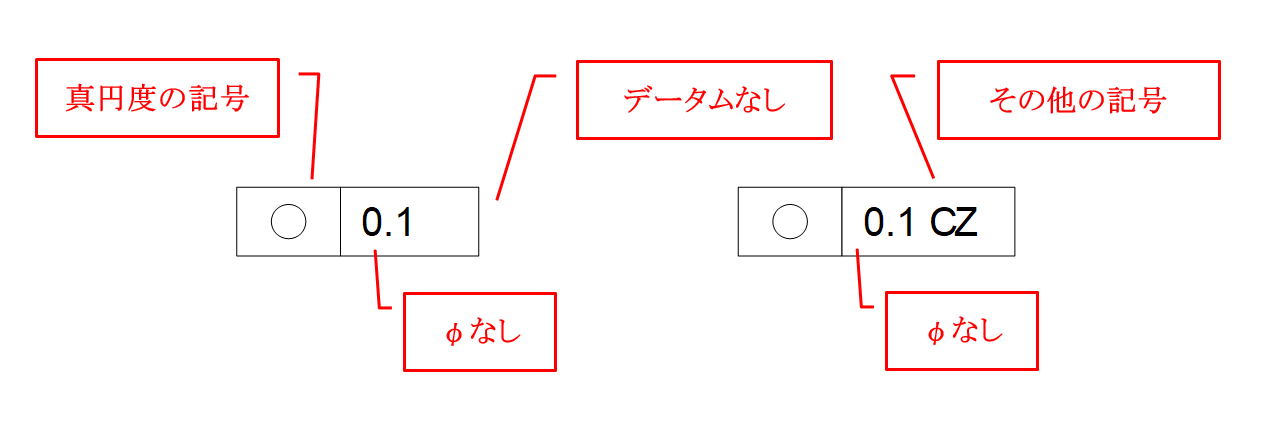
図7-2 真円度の記入例
真円度の対象となる形体は円筒形体の断面円です。従って、その断面円形体を包み込む同心2円間が公差領域となります。公差領域が隙間になることから幾何公差値にφを使うことはありません(図7-3)。
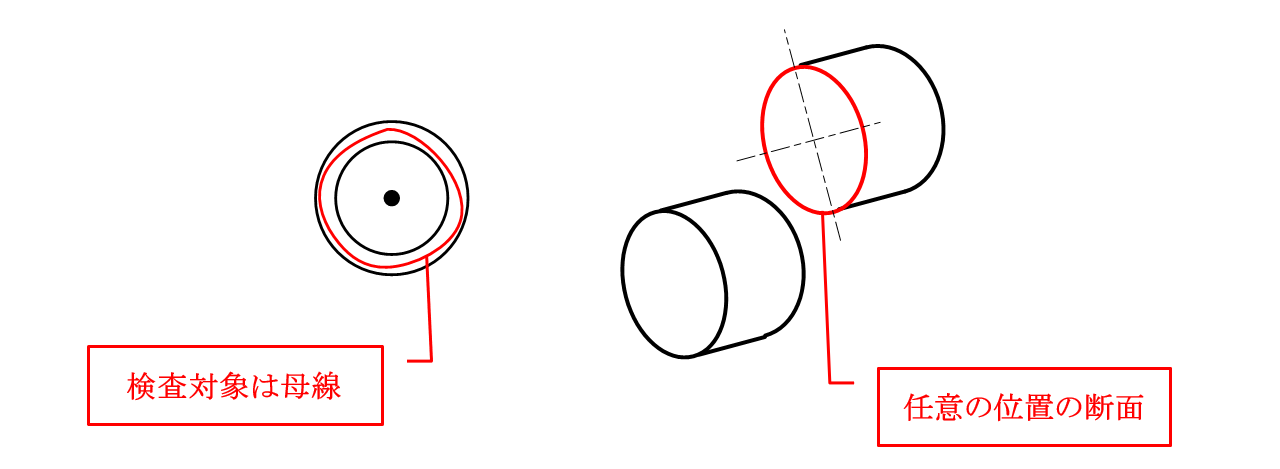
図7-3 真円度の公差領域のパターン
4. 真円度を適用する形状
真円度を適用する形状は、円筒面のある軸や球体に指示します(表7-1)。
表7-1 真円度を適用する形状例
| 適用する形状例 | データム | 対象形体 | 補助記号 | ||
| 1 | 円筒軸
円筒穴 |
|
不要 |
円形母線
(断続形体)
|
–
(CZ) |
| 2 | テーパー軸
ひょうたん軸 |

|
不要 |
円形母線
(断続形体)
|
–
(CZ) |
| 3 | 球 |  |
不要 | 円形母線
(断続形体) |
–
(CZ) |
| ~ コーヒーブレイク ~ “真球度”って言葉を使っていませんか? ボールベアリングに内蔵されている球は大変精度の高い直径サイズと球体形状が要求されます。設計の中で球体を使う場合、つい「真球度(しんきゅうど)」という言葉を使うことがあります。残念ながら幾何特性の中に「真球度」という特性は存在しません。真の球体を要求する場合、真円度あるいは輪郭度を使うしか手段がありません。 |
私見ですが、一般的な産業機械の部品に真円度を指示することは少ないと思います。なぜなら、軸は旋盤加工することが一般的であるため、真円から大きく形が崩れて楕円形や異形になることはほとんどありません。
逆に軸に比べると穴の方が真円度は崩れやすくなります。例えば精度を要求しないキリ穴はドリル加工され、ドリル刃の芯が振れた状態で加工すると“おむすび形”の穴が開く時があります(図7-4)。
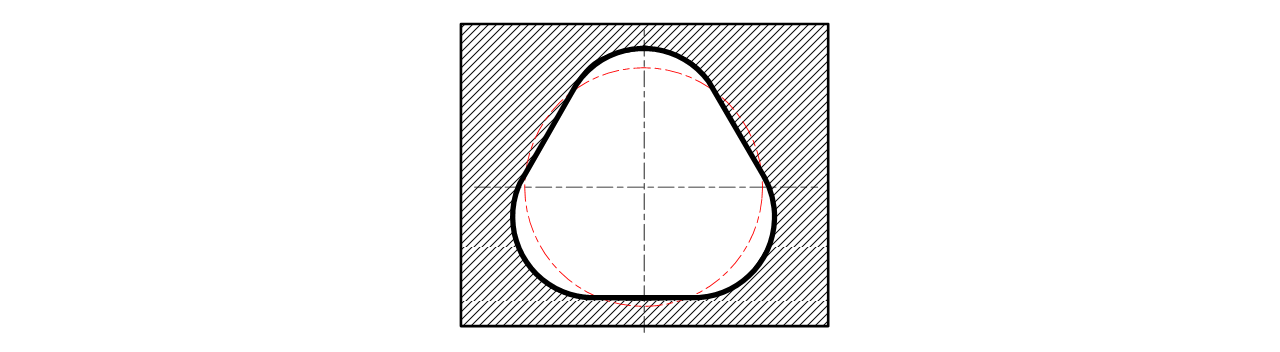
図7-4 ドリル加工でおむすび形に崩れた穴
しかし精度を要求するH7のようなはめあい公差の場合、リーマという仕上げ専用の刃物を使って最終加工するため寸法精度に加えて真円度も良好なものが得られます。
いずれにせよ、加工条件から軸よりは穴の方が、真円度は崩れやすいと覚えておくとよいでしょう。
5. 真円度の図面と公差領域
図面に真円度を指示する場合の設計意図と図面指示例、公差領域を解説します。
1) 円筒に真円度を指示する場合
設計意図
軸に歯車を圧入する際、圧入時の接触面積率を向上させて要求される回転トルクを保証したい(図7-5)。
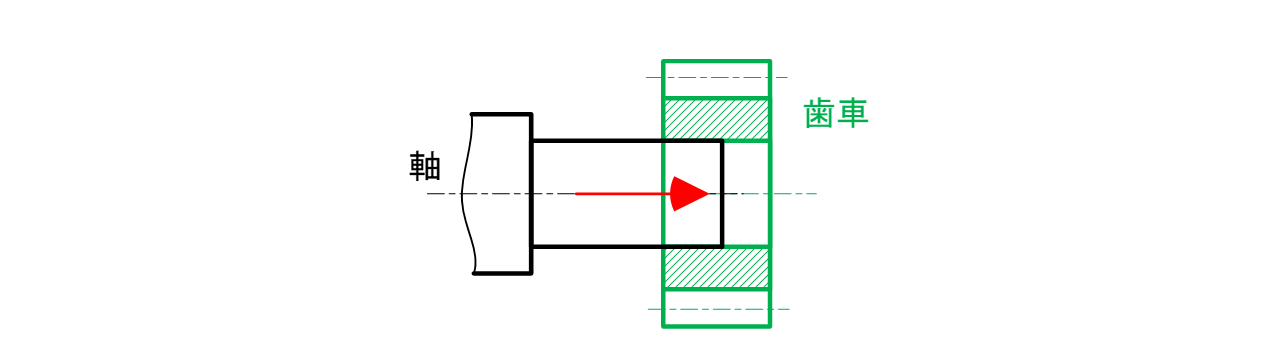
図7-5 軸に歯車を圧入して回転トルクを保証したいという設計意図
図面指示(軸)
挿入する円筒の直径寸法の矢と明確に外して真円度を指示します(図7-6)。
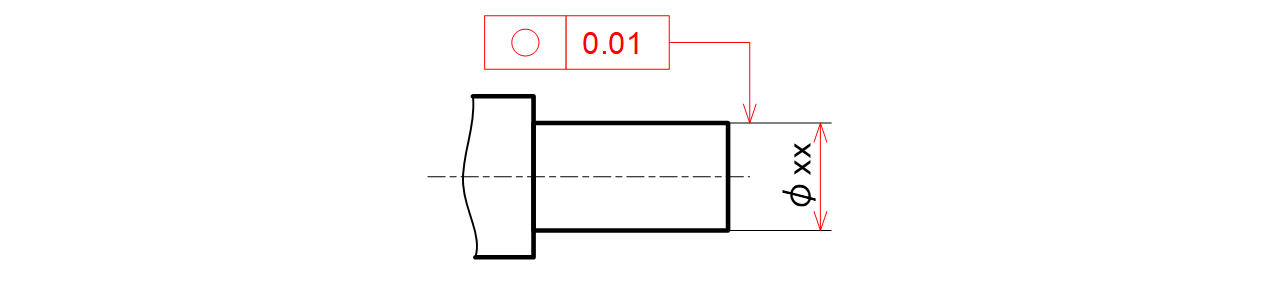
図7-6 軸に指示した例
公差領域(軸)
0.01mm離れた同心2円間の領域で規制されます(図7-7)。
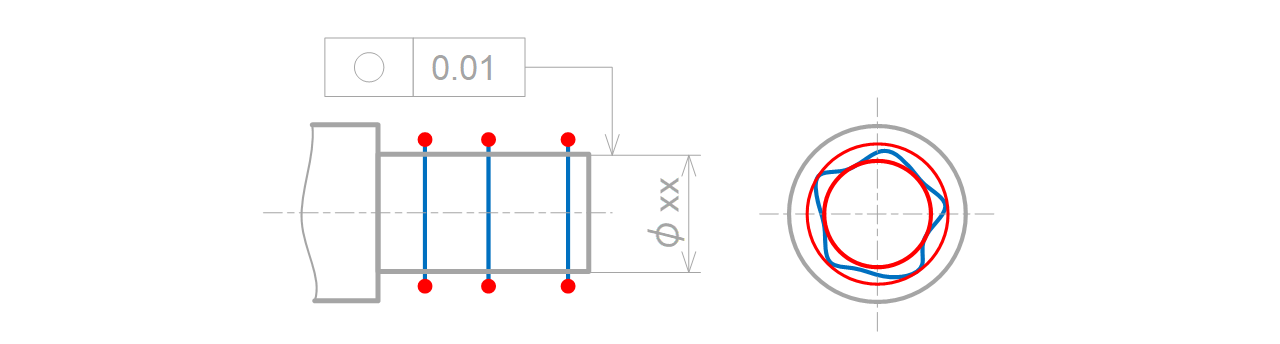
図7-7 軸に指示した時の公差領域
図面指示(歯車)
穴の直径の寸法線の矢と明確に外して真円度を指示します。指示線や矢の向きは穴の裏面から指示しても表面から指示しても構いません(図7-8)。
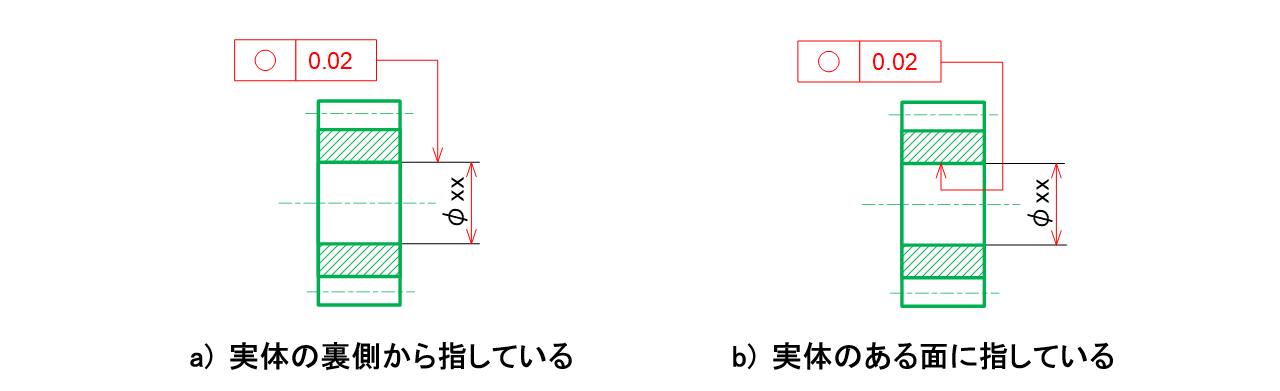
図7-8 穴に指示した例
公差領域(歯車)
0.02mm離れた同心2円間の領域で規制されます(図7-9)。
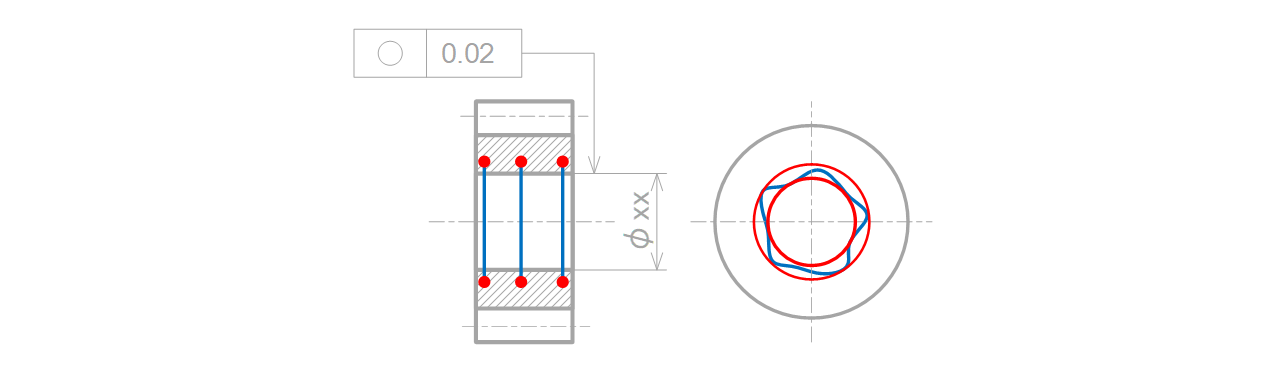
図7-9 穴に指示した時の公差領域
2) テーパーに真円度を指示する場合
設計意図
部品①のテーパー穴に軸のテーパーを接合する際、互いの面をできるだけ密着させたい(図7-10)。
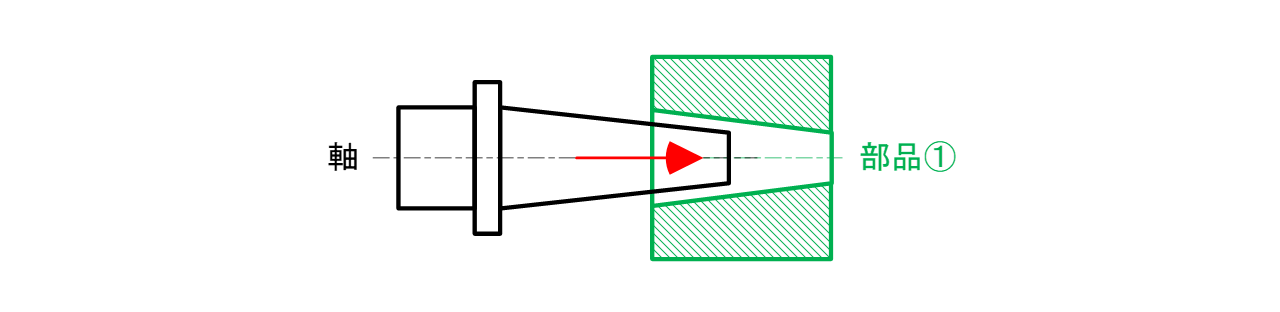
図7-10 テーパーの軸と穴を互いに挿入して密着させたいという設計意図
図面指示(軸)
テーパー軸の角度寸法の矢と明確に外して真円度を指示します(図7-11)。
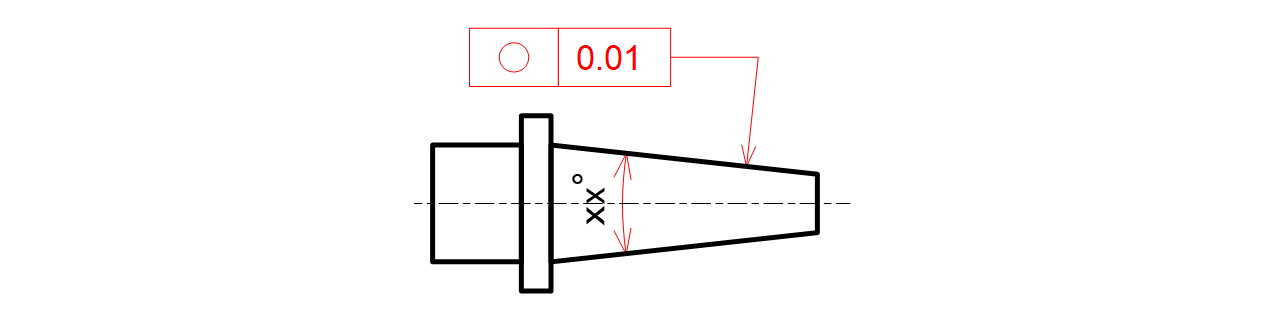
図7-11 テーパー軸に指示した例
公差領域(軸)
0.01mm離れた同心2円間の領域で規制されます。真円度は断面形状を評価するため、断面位置が異なることによる直径サイズの変化は問いません(図7-12)。
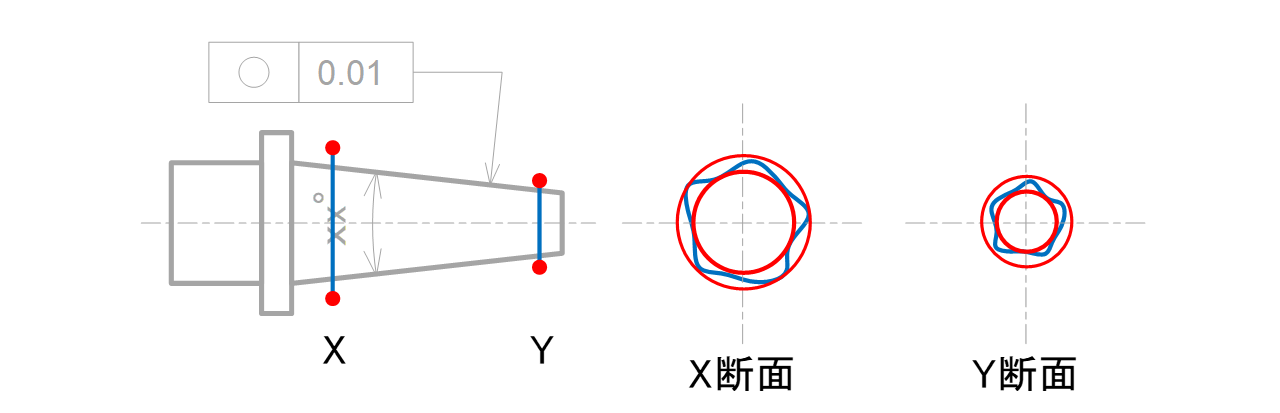
図7-12 テーパー軸に指示した時の公差領域
図面指示(部品①)
挿入するテーパー穴の角度寸法線の矢と明確に外して真円度を指示する(図7-13)。
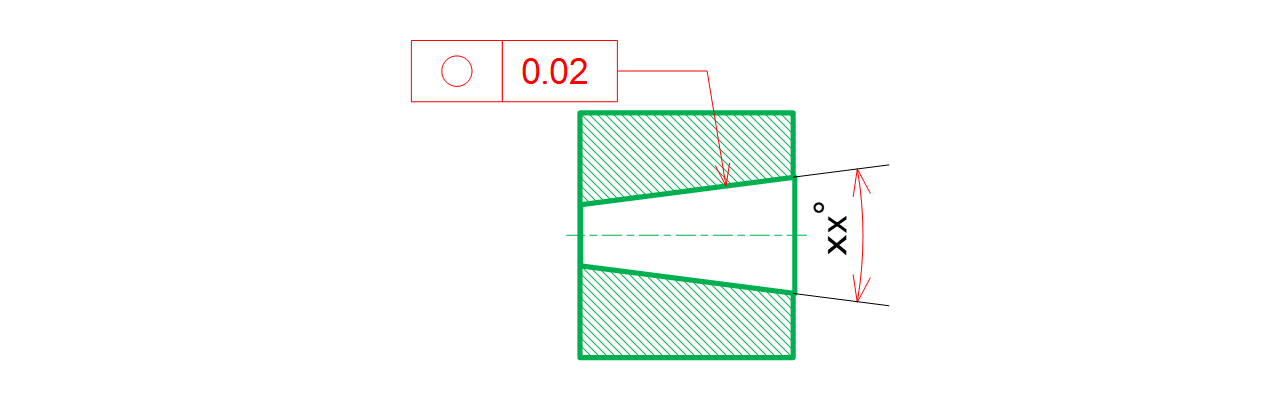
図7-13 テーパー穴に指示した例
公差領域(穴側)
0.02mm離れた同心2円間の領域で規制されます(図7-14)。
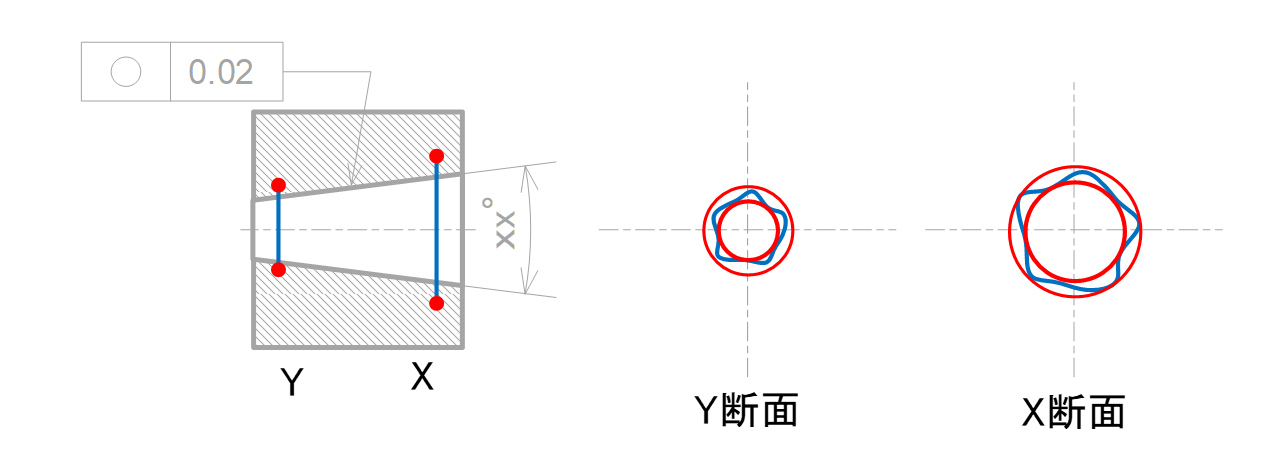
図7-14 テーパー穴の中心線に指示した時の公差領域
6. 真円度の検査方法
真円度測定機による測定
軸の真円度を測定する場合、その名を示す通り真円度測定機が最適といえます。
真円度測定機に軸を鉛直方向にセットし、テーブルを回転させながら任意の母線(赤色の線)を複数個所測定します。
JISには何か所測定するかどうかの指針は示されていないため、各企業内で測定個所の数を決めなければいけません(図7-15)。
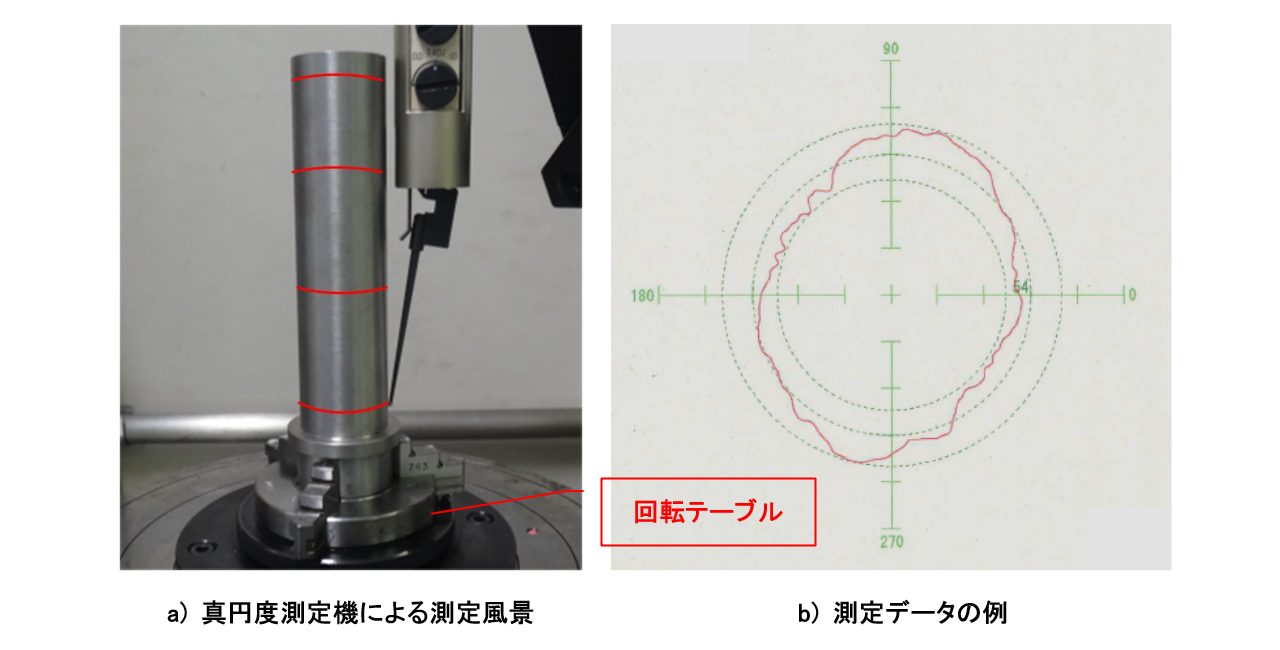
図7-15 真円度測定機による計測例
まとめ
今回は、真円度を指示する際のルールについて解説しました。
真円度は主に円筒軸や円筒穴に使うことが一般的です。公差領域が同心2円に挟まれた領域となることから、軸や穴の任意の位置での断面を評価することになります。
幾何学的に正しい真円からどのくらい崩れているかを評価することから、サイズの違いは問いません。そのためテーパー軸やひょうたん軸にも使うことができ、自由度の高い特性であると言えます。
真円度を真円度測定機で測定するイメージも知ることができ、母線そのものを評価していることがわかったと思います。
次回は、真直度や平面度、真円度と同じ形状偏差のグループに属する円筒度について解説します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >