位置度の記号は
「ライフルスコープのターゲットマーク」と覚える
本シリーズでは、グローバル図面に不可欠な「幾何公差」の意味と、図面におけるルールについて解説しています。第17回となる今回は、「位置偏差」グループに含まれる位置度に焦点を当て、その意味や記号の使い方について詳しくご紹介します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >
目次
1.位置偏差とは
位置偏差は関連形体に分類され、データムに関連して幾何偏差が決められる形体になります。位置偏差には次の5つの幾何特性があります。
・同軸度/同心度
・対称度
・位置度 ←今回解説する幾何特性
・線の輪郭度…位置偏差の場合、データムに関連する
・面の輪郭度…位置偏差の場合、データムに関連する
2.位置度とは
位置度は「データムまたは他の形体に関連して定められた理論的に正確な位置からの点、直線形体または平面形体の狂いの大きさ」とJISで規定されます。
位置度はデータムありで指示することが一般的ですが、データムなしで指示することもできます。
位置度は、点・直線または平面に適用されます。検査対象が直線や平面ではない場合には次回解説する線の輪郭度または面の輪郭度を用います。
3. 位置度の記号と記入のルール
位置度を図面に表現する場合、公差記入枠に位置度の記号と幾何公差値、必要に応じてその他の記号・データム記号を記入します。公差記入枠は2つあるいは3つ以上の区画のものを使います(図17-1)。
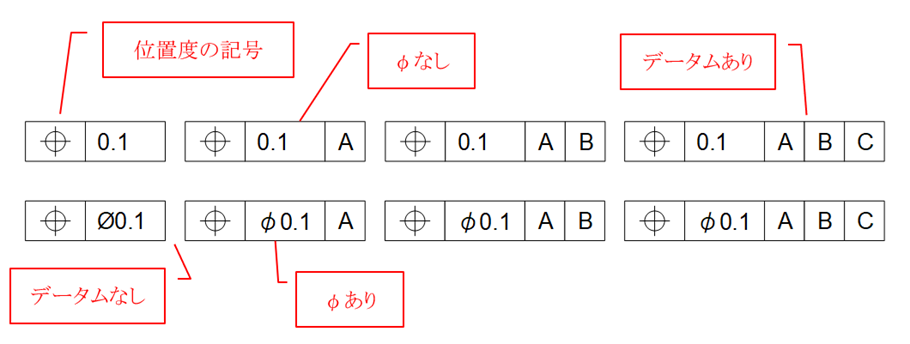
図17-1 位置度の記入例
位置度の対象となる形体は平面または中心平面・中心線・中心点で、これらの形体を包み込む空間が公差領域となります。公差領域に応じて幾何公差値にφが付かない場合とφが付く場合があります(図17-2)。
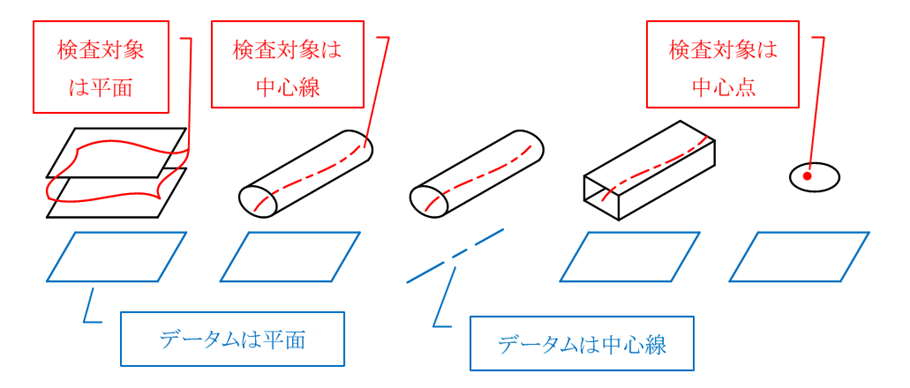
図17-2 位置度の公差領域のパターン例
4. 位置度を適用する形状
位置度を適用する形状は、データムから離れた位置にある平面や中心平面、中心線などに指示します(表17-1)。
表17-1 位置度を適用する形状例
| 適用する形状例 | データム | 対象形体 | 補助記号 | ||
| 1 | 平面
断続平面 (同一面) |
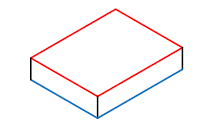 |
要 | 平面
(断続形体) |
–
(CZ) |
| 2 | 穴(複数可)
断続穴 (同一穴) |
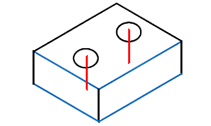 |
要 | 中心平面
(断続形体) |
–
(CZ) |
| 3 | 穴(複数可)
|
 |
なくても可 | 中心点
|
–
|
| 4 | 溝
断続平面 (同一面) |
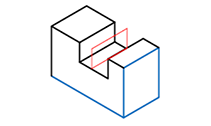 |
要 | 中心平面
(断続形体) |
–
(CZ) |
| 5 | 球体
|
 |
要 | 中心点
|
–
|
5. 位置度を指示する前段階の考え方
1) XY座標の公差値が同じ場合
位置度を指示する際に、従来の寸法公差方式で記入されている図面を参考あるいはイメージしてから位置度に描き変えるようにするとわかりやすくなります。
例えば、公差幅はXY座標方向ともに±0.1(公差幅0.2mm)の公差値で従来の寸法公差方式で記入された図面を考えます(図17-3)。

図17-3 従来の寸法公差方式の公差指示例
図17-3の図を位置度に描き変える手順を確認しましょう(図17-4)。
①相手部品との接触面をデータムとして設定します。
②位置の寸法数値を理論的に正確な寸法で記入します。
③位置ずれを許容するために公差記入枠に位置度と公差値を記入します。
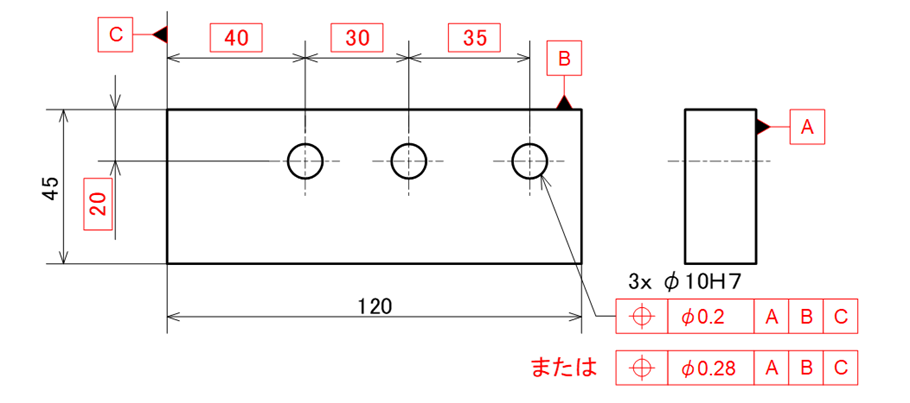
図17-4 従来の寸法公差方式を位置度公差に描き直した例
図17-4で、幾何公差値がφ0.2とφ0.28の2種類が示されており、これらの数値の根拠を説明します。
従来の寸法公差方式の図では穴位置の公差がXY座標ともに「±0.1」で示されていることから、公差領域は0.2mmの正方形領域となります。
ところが正方形領域だと斜め45°の位置では最大0.28mmずれても問題ないことになって公差値との矛盾が生じてしまいます(図17-5)。

図17-5 従来の寸法公差方式の公差領域イメージ
設計意図として「従来の寸法公差方式では最大で0.28mmの位置ずれを許していたんだから全方向でφ0.28mmずれてもよいことにしよう」と考えたら幾何公差値をφ0.28として構いません。逆に「累積公差の計算を0.2mmで検討したから0.28mmに広げると困る」という場合は幾何公差値をφ0.2とすればよいのです(図17-6)。
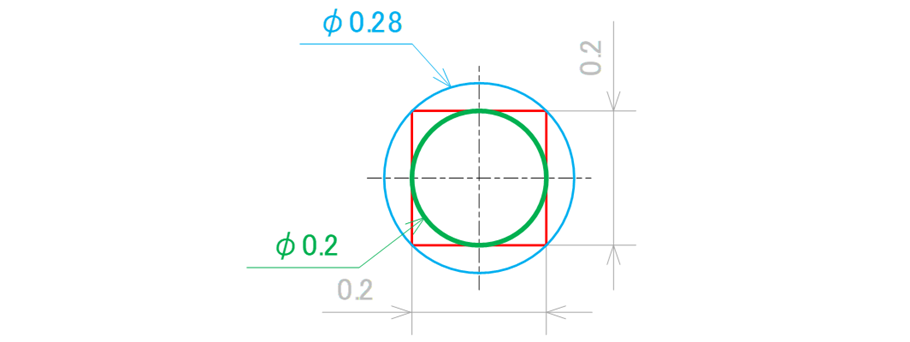
図17-6 設計意図との違いによる公差値の考え方の違い
2) XY座標の公差値が異なる場合
図17-3と異なり、XY座標方向の公差値が異なる従来の寸法公差方式で記入された図面を考えます(図17-7)。
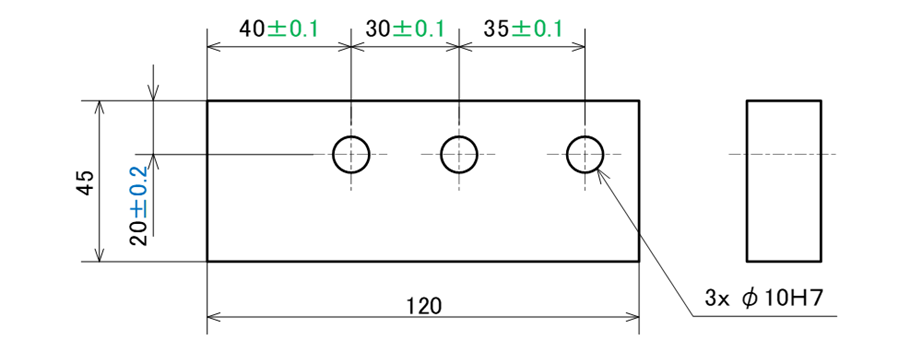
図17-7 従来の寸法公差方式の公差指示例
図17-7を位置度に描き変える手順を確認しましょう(図17-8)。
①相手部品との接触面をデータムとして設定します。
②位置の寸法数値を理論的に正確な寸法で記入します。
③位置ずれを許容するためにX座標を表すために横向きの寸法線(緑色)の延長線上に公差記入枠(位置度と公差値0.2)を、Y座標を表すために縦向きの寸法線(青色)の延長線上に公差記入枠(位置度と公差値0.4)を記入します。

図17-8 位置度を使った公差指示例
図17-8はXY座標で異なる公差値の領域を示しています(図17-9)。
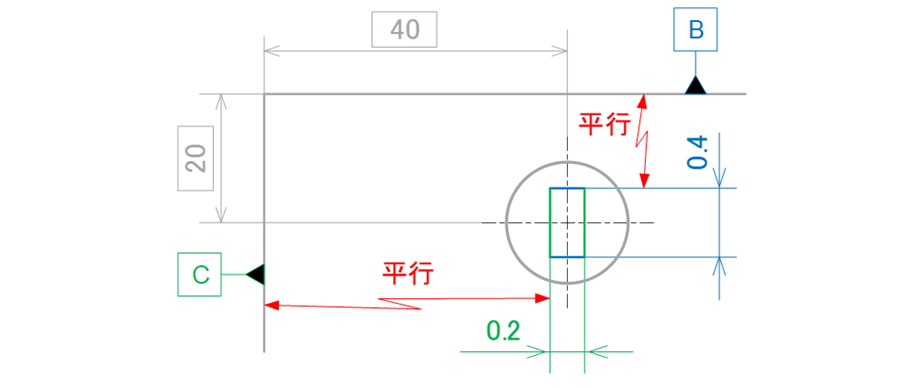
図17-9 従来の寸法公差方式を位置度公差に描き直した例
ここで図17-4と図17-8とで、データムBとデータムCはそれぞれX座標面・Y座標面を生成していることがわかります。それではデータムAは何を示しているのでしょうか?
図のデータムAはZ軸座標面を表しており、図17-4では公差領域φ0.2またはφ0.28の円筒に対する直角度を、図17-8では公差領域0.2×0.4の角柱に対する直角度を意味しているのです。
つまり位置偏差には姿勢偏差(平行度・直角度・傾斜度)も同時に含んでいることがわかります。
6. 位置度の図面と公差領域
図面に位置度を指示する場合の設計意図と図面指示例、公差領域を解説します。
1 部品の穴と台座の穴に軸を挿入する場合
設計意図
部品を台座に固定した後、部品と台座の2つの穴に軸を挿入したい(図17-10)。
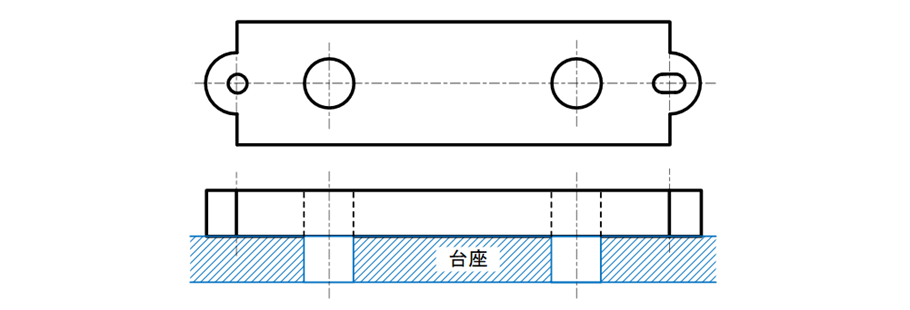
図17-10 部品を台座に固定した後、2本の軸を挿入したいという設計意図
図面指示
部品と台座の接触面をデータムとして指示しますが、裏表同形状でどちらが接触面になるかわからないため中心平面にデータムAを設定します。
次に左側にあるφ6.1穴が取付の位置決め穴になるため、穴の中心線にデータムBを設定します。次に右側にある長穴で部品の周り止めとするため、長穴の中心平面にデータムCを設定します。
最後に中央にある2つの大きな穴に位置度を指示します(図17-11)。
※データムBであるφ6.1穴や幾何公差が指示されているφ16H7の寸法の矢が片方だけであり母線指示のように見えますが、ISOによると小径穴に寸法の矢を片方だけで指示すると中心線指示解釈できるようです。

図17-11 位置度を指示した例
公差領域
検査対象となる穴の中心線は、データムAに対して直角を、データムBとデータムCが作る座標面上でデータムBからの位置が30.00mm、さらにそこから80.00mmの位置にある直径0.03mmの円筒領域で規制されます。
2つの穴のY軸方向の理論寸法「0」(緑色)は、製図のルールとしてゼロは省略するため図面には表現されていません(図17-12)。
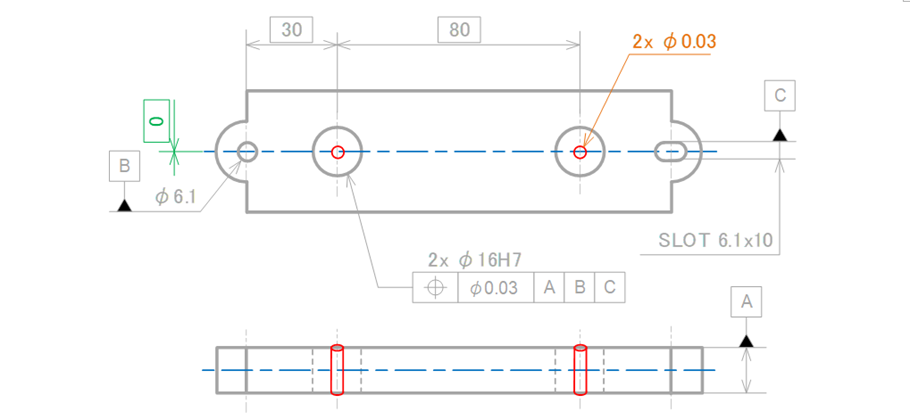
図17-12 位置度を指示した時の公差領域
2 6つの取り付け穴をもつ部品①を台座に固定する場合
設計意図
6つの取り付け穴をもつ部品を表裏関係なく台座のインロー部に取り付ける際、6つの穴が台座のねじ穴の位置に合いボルトで固定したい(図17-13)。
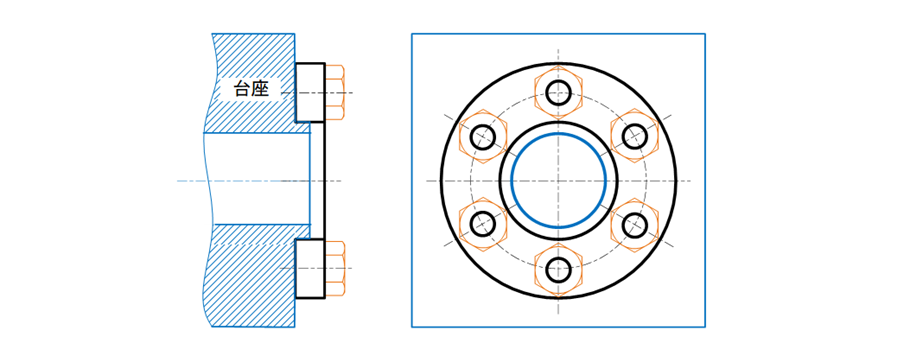
図17-13 部品を台座のインロー部に挿入し6つ穴でボルト固定したいという設計意図
図面指示
部品と台座の接触面をデータムとして指示しますが、裏表同形状でどちらが接触面になるかわからないため中心平面に第一優先データムA記号を付けます。インロー合わせするφ40H7穴の中心線に第二優先データムB記号を付けます。6つの穴の中心線に位置度を指示します(図17-14)。
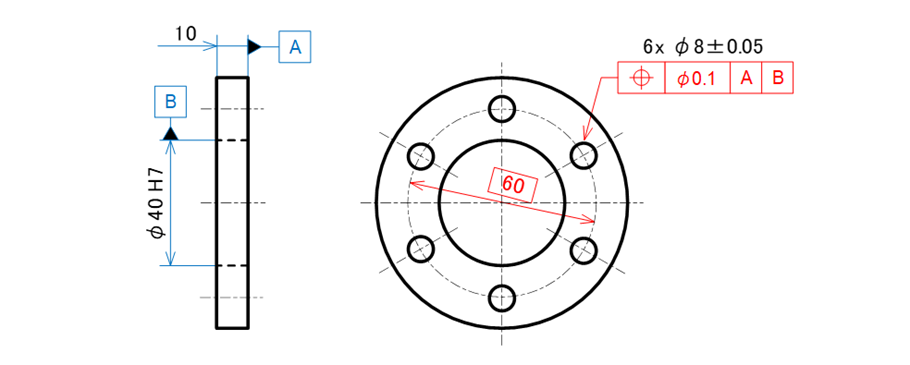
図17-14 位置度を指示した例
公差領域
検査対象となる6つの中心線は、データムAに対して直角を、データムBを中心とする60.00mmのピッチ円上に6等分された位置にある直径0.03mmの円筒領域で規制されます。6つの穴の相対角度の理論寸法「60°」(緑色)は、製図のルールとして均等配置である場合は省略することができるため図面には表現されていません(図17-15)。
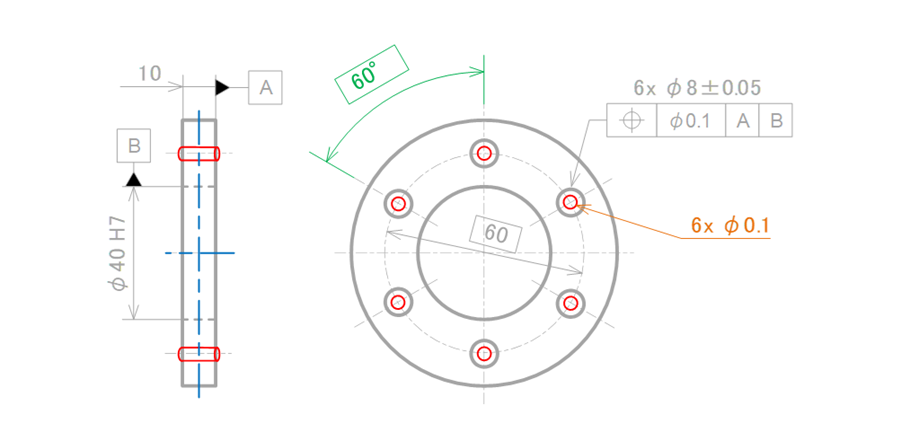
図17-15 位置度を指示した時の公差領域
7. 位置に対する片振り公差の考え方
多くの企業で穴位置に片振り公差(例:0~+0.1)を付けた図面が散見されます。筆者もそのような図面を何度も描いたことがあります。穴位置に片振り公差を付けるシチュエーションとして歯車のバックラッシ確保があります(図17-16)。

図17-16 歯車の軸間距離の寸法指示例
ISOを確認する限り、片振り公差はサイズに対してのみ行い、位置に対しては行っていません。サイズは互いにガタを最小限あるいは圧入で嵌め合うという設計意図に対して片振り公差の指示が必要です。位置に関しては設計意図として「ど真ん中を狙う!」が必須条件であるはずだからです。
したがって、図17-16の図を位置度公差で表す場合、次のように穴間距離の理論的に正確な寸法は中央値の「30.05」で指示するしか手段がありません(図17-17)。
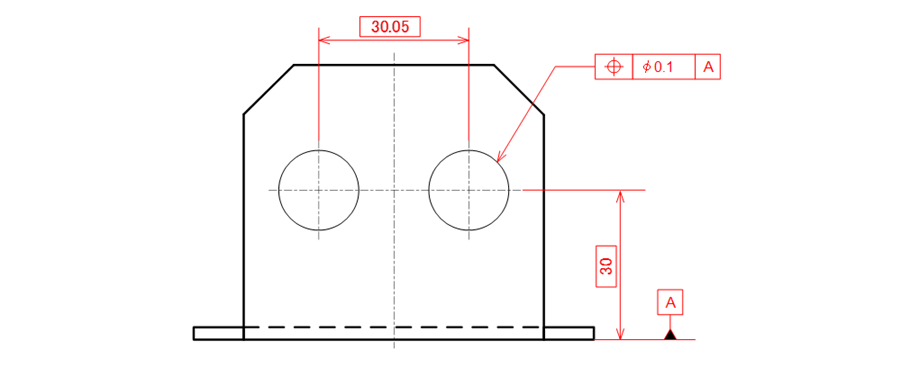
図17-17 穴間距離の理論的に正確な寸法を中央値に補正して指示した例
コーヒーブレイク
板金をプレスで打ち抜く際にカエリ面やダレ面が生じることは、「ザ・メカニカル・ドローイング 我流と本流-製図のお作法-」の「薄くて弱いが、とても安い加工法だ。おまえに板金が扱えるか‐荷重の向きと曲げの考え方」の記事の項番5で説明した通りです。
基準となるデータム面にカエリが出ていると、製品への組付け時や検査の際の実用データムとなる定盤に置いた際に部品が浮いたり傾いたりする恐れがあります。
そのため、データム面には「ダレ面」あるいは「カエリ無きこと」のような注意事項を明記しなければいけません。
8. 位置度の検査方法
CNC3次元測定機による位置度の評価
CNC3次元測定機を使用して位置度を測定する際の検査の理屈を説明します(図17-18)。
①データムA面の測定[図17-18 b)]
データムAで指示されている面を定盤に押し当て、実用データムである定盤の面を測定してデータムAと設定します。
②データムB面の測定[図17-18 c)]
データムBで指示されている分離した二面を測定して共通領域としてデータムBと設定します。
③データムC面の測定[図17-18 d)]
データムCで指示されている面を測定してデータムCと設定します。
④位置度の測定[図17-18 e)]
位置度で指示されている穴の円周面のデータを測定し、穴の中心線を演算によって割り出してデータムAに対して直角かつ、データムBとデータムCからの理論的に正確な距離とのずれ量を測定します。
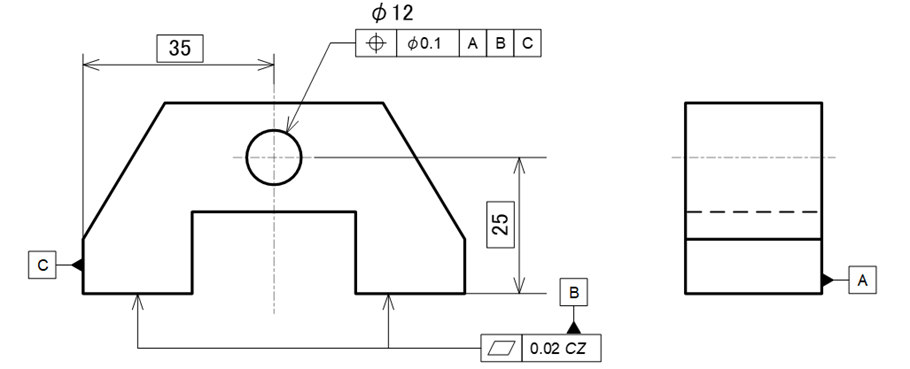
a)図面指示例

b)データムAの設定
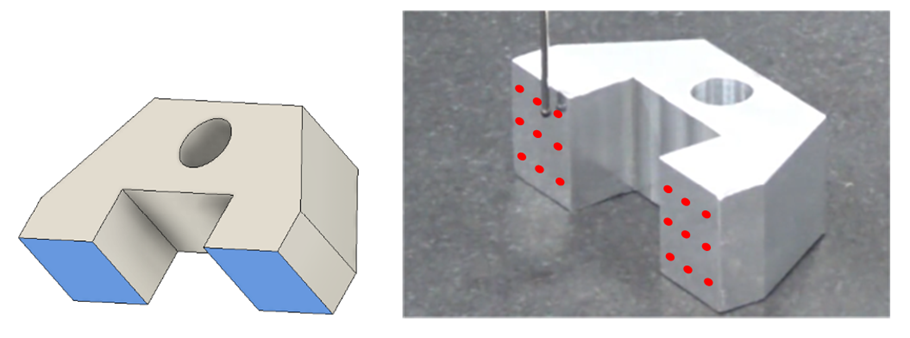
c)データムBの設定
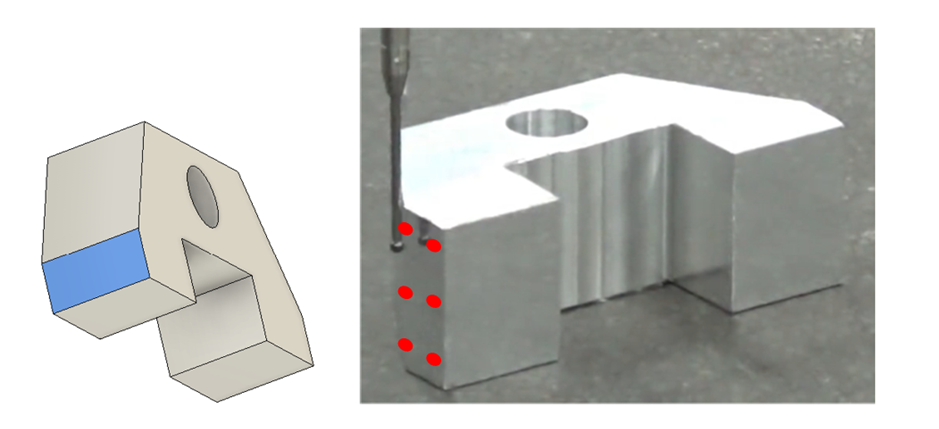
d)データムCの設定
 a) 穴の下側の円筒面を触る |
 b) 穴の上側の円筒面を触る |
e) 位置度の測定
図17-18 CNC3次元測定機による位置度測定の例
まとめ
今回は、位置度を指示する際のルールについて解説しました。
設計意図として位置はど真ん中狙いであるべきことから、従来の寸法公差のような片振り公差ができず、位置を示す理論的に正確な寸法は中央値で指示するしか手段がないことも知りました。
位置度はCNC3次元測定機で測定することができます。
次回は、同軸度/同心度や対称度、位置度と同じ位置偏差のグループに属し、複雑な形状の指示に適する線の輪郭度と面の輪郭度について解説します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >






