円周振れの記号は
「ダイヤルゲージの針」と覚える
このシリーズでは、グローバル図面に必須の幾何公差について、その意味や図面のルールをわかりやすく解説しています。
今回のテーマは 「円周振れの意味と記号の使い方」。
前回の位置偏差に続き、今回は4つ目のグループである 振れ偏差 に焦点を当て、その中でも重要な 円周振れ について詳しく説明します。
円周振れの基本的な考え方、記号の正しい使い方、設計や製造で押さえておきたいポイントをまとめました。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >
目次
1.振れ偏差とは
振れ偏差は関連形体に分類され、データムに関連して幾何偏差が決められる形体になります。
振れ偏差には次の2つの幾何特性があります。
・円周振れ ←今回解説する幾何特性
・全振れ
2.円周振れとは
円周振れは「データム軸直線を軸とする回転面をもつべき対象物またはデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した位置または任意の位置で指定した方向(*)に変位する大きさ」と定義されます。円周振れはデータムを必要とします。
(*)指定した方向とは,データム軸直線と交わりデータム軸直線に対して垂直な方向(半径方向),データム軸直線に平行な方向(軸方向)またはデータム軸直線と交わりデータム軸直線に対して斜めの方向(斜め法線方向及び斜め指定方向)をいう。
3.円周振れの記号と記入のルール
円周振れを図面に表現する場合、公差記入枠に円周振れの記号と幾何公差値、必要に応じてその他の記号、データム記号を記入します。公差記入枠は3つ以上の区画のものを使います(図19-1)。

図19-1 円周振れの記入例
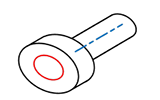
円周振れの対象となる形体は、データム中心線を基準に回転した際の円筒上の母線や軸直角端面の母線です。従って、その母線が通過できる2点間が公差領域となります(図19-2)。
図19-2 円周振れの公差領域のパターン
4.円周振れを適用する形状
円周振れを適用する形状は、真っ直ぐな円筒面に加えて、テーパー軸やひょうたん形の軸、あるいは軸直角方向の平面やテーパー、球面などに指示します(表19-1)。
表19-1 円周振れを適用する形状例
| 適用する形状例 | データム | 対象形体 | 補助記号 | ||
| 円周振れ | 円筒上の 母線 |
 |
要 | 母線
(断続形体) |
–
(CZ) |
| テーパー軸 |
|
要 | 母線
(断続形体) |
–
(CZ) |
|
| ひょうたん形の軸 |
|
要 | 母線
(断続形体) |
–
(CZ) |
|
| 軸直角平面 |
|
要 | 母線
(断続形体) |
–
(CZ) |
|
5.円周振れの図面と公差領域
図面に円周振れを指示する場合の設計意図と図面指示例、公差領域を解説します。
① 円筒面に円周振れを指示する場合
設計意図
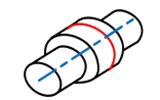
両端を軸受で支持された軸が回転した際に断続する円筒面と相手部品との間隔を保証したいために円筒面が振れて欲しくない(図19-3)。

図19-3 軸受で支持された断続する円筒面が振れて欲しくないという設計意図
図面指示
2つの軸受で支持されている2本の軸部の中心線を共通データム「A-B」として指示します。共通データム「A-B」を中心に回転したときに振れを規制したい断続する円筒面に円周振れを指示します(図19-4)。
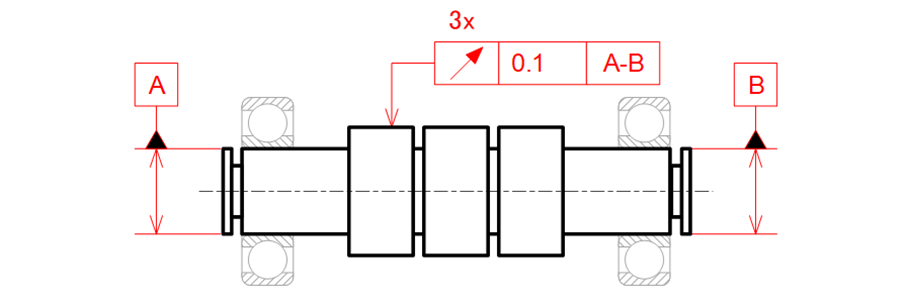
a) 指示部を個数表記した例

b) 指示部のそれぞれに矢を示した例
図19-4 円周振れを断続する円筒面に指示した例
公差領域
検査対象となる任意の位置の円形母線は共通データムA-Bの中心線基準で回転したとき、任意の測定位置におけるデータム軸に直角な0.1mm離れた2円間の領域で規制されます(図19-5)。

図19-5 円周振れを円筒面に指示したときの公差領域
② 円すい面に円周振れを指示する場合
設計意図
2つの軸受で支持された片持ち軸が回転した際に円すい面と相手部品の円すい穴との間隔を保証したいために円すい面が振れて欲しくない(図19-6)。

図19-6 軸受で支持された軸の円すい面が振れて欲しくないという設計意図
図面指示
2つの軸受で支持されている部分の中心線を共通データムA-Bとして指示します。共通データムA-Bを中心に回転したときに振れを規制したい部分に円周振れを指示します(図19-7)。

図19-7 円周振れを円すい面に指示した例
公差領域
検査対象となる任意の位置の母線は共通データムAの中心線基準で回転したとき、任意の測定位置におけるデータム軸に直角な0.1mm離れた2円間の領域で規制されます(図19-8)。

図19-8 円周振れを円すい面に指示したときの公差領域
6.円周振れの検査方法
真円度測定機による測定
データムを参照する必要があるため、真円度測定機によって測定することができます(図19-9)。

a)円筒面の円周振れ測定

b)軸直角端面の円周振れ測定
図19-9 真円度測定機による測定
Vブロックとダイヤルゲージによる測定
データム部分をVブロックで支持し、手で軸を回転しながらダイヤルゲージの振れ幅を見ることで測定することができます(図19-10)。

図19-10 Vブロックとダイヤルゲージによる測定
7.円周振れと真円度、同軸度との違い
検査の視点による違い
設計の視点による違い
まとめ
今回は、振れ偏差に属する円周振れを指示する際のルールについて解説しました。
円周振れは真円度測定機やVブロックとダイヤルゲージの組み合わせで測定できることがわかりました。
円周振れは、データム中心線を基準として軸を回転したときの母線の振れ幅を見ることがわかったと思います。
次回は、14種類の特性の最後となる全振れについて解説します。
meviy 2D|PDF図面アップロードで簡単操作
かんたん見積もりはこちらから >