
機械設計の現場において、材料の「ヤング率(縦弾性係数)」は、部品の剛性や変形量を決定づける重要な特性です。しかし、強度(引張強さ)との混同や、ハイテン材(高張力鋼)に対する誤解などにより、適切な材料選定や設計計算が行われないケースも少なくありません。
本記事では、ヤング率の定義やフックの法則といった基礎理論はもちろん、単位換算や主要材料の数値データ、片持ち梁を用いたたわみ計算の実践について解説します。設計品質を確実に担保し、手戻りのない設計を行いたい方は最後までご覧ください。
目次
ヤング率(縦弾性係数)とは?
まずはヤング率(縦弾性係数)の物理的な意味や定義、実務で扱う単位系について、理解しておきましょう。
一言で言うと「バネの硬さ」
物理学における「フックの法則」は、バネの伸びが荷重に比例することを示しています。ヤング率とは、この法則を材料に適用した指標であり、「材料そのものが持つバネの硬さ」と定義可能です。
- ヤング率が大きい = 変形しにくい(硬いバネ、鉄やセラミックスなど)
- ヤング率が小さい = 変形しやすい(柔らかいバネ、ゴムや樹脂など)
「縦弾性係数」とも呼ばれますが、設計実務の現場では一般的に「ヤング率」と呼ばれます。引張や圧縮の荷重を受けた際、材料がどの程度伸縮するかを決定する基本的な定数です。
定義と計算式(フックの法則)
ヤング率の定義は、弾性範囲内における応力(σ)とひずみ(ε)の比例関係に基づきます。ヤング率Eはその比例定数であり、以下の関係式で表されます。
σ=E×ε
ここで、応力σは材料内部に生じる単位面積あたりの力(MPaやN/mm2)、ひずみεは元の長さに対する変形量の割合(無次元、%表記など)です。
言い換えれば、ヤング率は
E=σ÷ε
で定義され、材料試験で得られる「応力–ひずみ線図(S-Sカーブ)」における弾性域(直線部分)の傾きがヤング率の値となります。
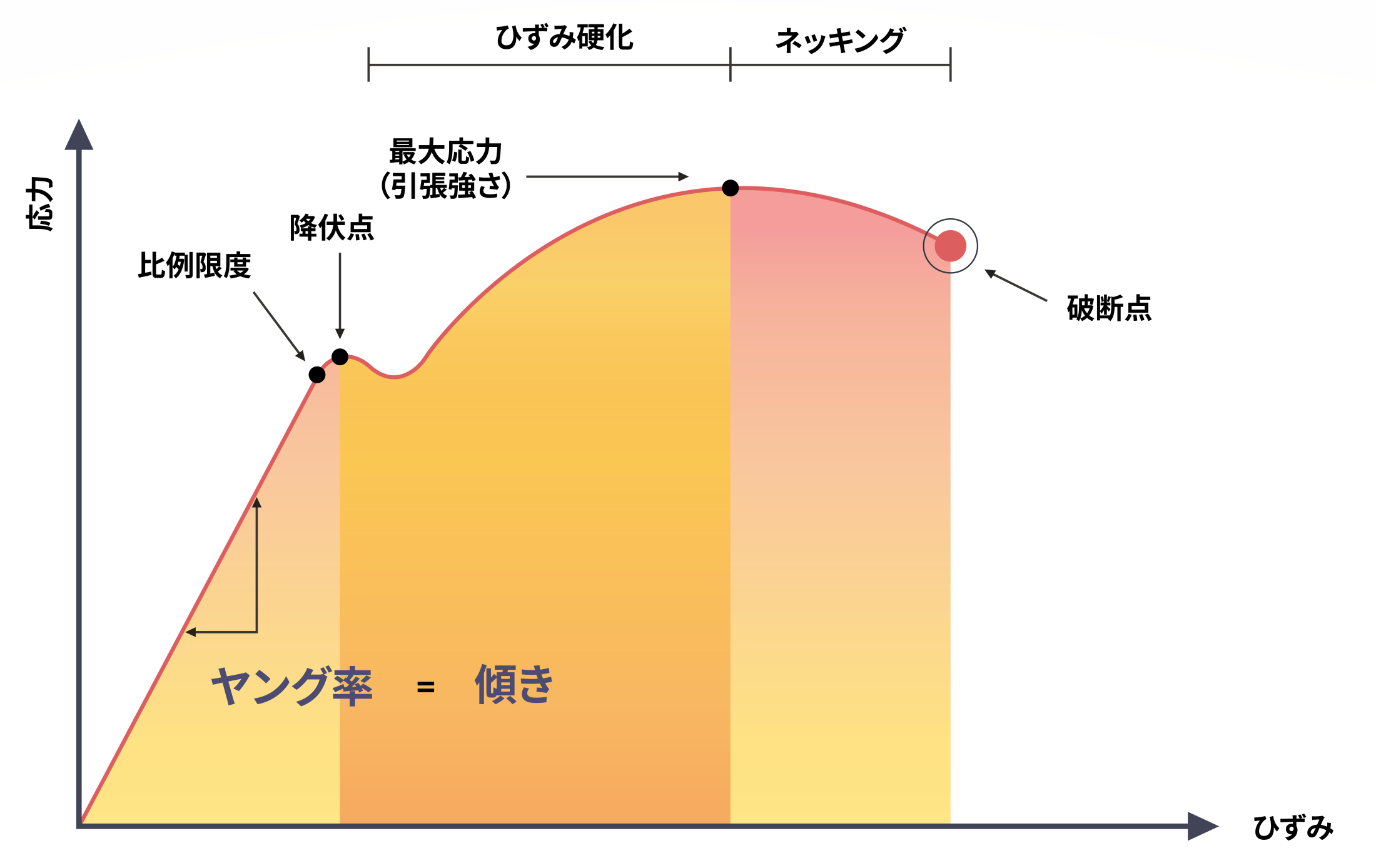
応力ひずみ曲線の例
ヤング率の単位と換算
ヤング率の単位は応力と同じくPa(パスカル)です。ただし実用上は値が大きくなるため、通常はMPa(メガパスカル)やGPa(ギガパスカル)が使われます。
また、古い工学単位系ではkgf/mm²やkgf/cm²が用いられる場合もあるため、設計者は各単位の関係を把握しておかなければなりません。以下に主要単位の換算関係をまとめます。
- 1 Pa=1 N/m²(SI基本単位)
- 1 MPa=1 N/mm²(工学単位。N/mm²とMPaは等価)
- 1 GPa=1,000 MPa=1,000 N/mm²
- 1 kgf/mm²≒9.81 MPa(厳密には80665 MPa)
- 1 MPa≒0.102 kgf/mm²(1 N≒0.10197 kgfより算出)
実務用・単位早見表
| 単位 | MPa(N/mm2) | GPa | kgf/mm² |
| 1 MPa | 1 | 0.001 | 約 0.102 |
| 1 GPa | 1000 | 1 | 約 102 |
| 1 kgf/mm² | 9.80665 | 0.0098 | 1 |
例えば、一般的な鉄鋼材料のヤング率は約205 GPaですが、他の単位で表すと205,000 MPaや約20,900 kgf/mm²となります。
【重要】換算の目安
厳密な計算を要しない場面では、以下の近似値を用いることで見積もりが可能です。
1 kgf/mm2≒9.8 MPa
「ヤング率(剛性)」と「引張強さ(強度)」の違い
材料選定において混同されやすく、設計ミスにつながるのが「剛性」と「強度」の取り違えです。設計品質を確保するために、それぞれの役割を明確に理解しておきましょう。
変形しにくさと、壊れにくさは別物
一言で言えば、剛性は「変形のしにくさ」を、強度は「壊れにくさ」を表します。
- 剛性
- 指標:ヤング率
- 意味:所定の荷重に対し、どれだけ歪む(たわむ)か
- 目的:精密な位置決めや変形抑制
- 強度
- 指標:降伏点、引張強さ
- 意味:所定の荷重に対し、いつ壊れる(破損・塑性変形する)か
- 目的:破壊や折損の防止
頑丈な部品と言ったとき、たわまない部品(高剛性)を指すのか、折れない部品(高強度)を指すのかによって、選ぶべき材料や設計手法は変わってきます。
高張力鋼(ハイテン)の落とし穴
設計現場で見られる誤解のひとつに、「強度の高い材料(ハイテンや焼入れ鋼)を使用すれば、たわみも減少する」というものがあります。これは誤りです。
一般的な軟鋼(SS400)であっても、最高強度の特殊鋼や熱処理されたハイテン材であっても、鉄鋼材料のヤング率は一律で約206 GPa です。材料の強度(降伏点や引張強さ)を2倍、3倍に高めても、ヤング率は変化しないため「変形のしにくさ」は向上しません。
もし「強い材料にしたから薄くしても大丈夫だろう」と板厚を薄くしてしまえば、強度は足りていても剛性不足に陥り、たわみ量は増大してしまいます。たわみ(剛性不足)を解決するためには、材料グレードの変更は効果がありません。板厚を上げる、リブを立てるなど「断面形状の変更(断面二次モーメントの増大)」が必要です。
【保存版】主な材料のヤング率一覧表
設計計算および材料選定の基礎データとして、代表的な材料のヤング率を以下に示します。
鉄鋼材料(Steel)
炭素鋼・低合金鋼では、ヤング率は鋼種や熱処理の有無で大きくは変わらず、概ね200~210 GPaの範囲で扱われます。
| 材料名 | ヤング率 (GPa) | 特徴・備考 |
| 軟鋼 (SS400) | 205 | 一般構造用圧延鋼材 |
| 炭素鋼 (S45C) | 205 | 機械構造用炭素鋼、軸部品等 |
| クロモリ鋼 (SCM435) | 210 | 強靭鋼、ボルトや高負荷部品 |
| 工具鋼 (SKD11) | 206 | 金型用鋼、高硬度だがヤング率は同等 |
| ステンレス (SUS304) | 193 | 炭素鋼に比べわずかに低い傾向 |
| 鋳鉄 (FC250) | 100 | 黒鉛を含むため、鋼の約1/2程度の値 |
※焼入れ・焼き戻し等の熱処理を行っても、硬さは変化しますがヤング率(剛性)は変化しません。
非鉄金属(Non-ferrous metals)
鉄以外の金属を採用する際は、鉄に対する剛性の比率を把握しておきましょう。
| 材料名 | ヤング率 (GPa) | 特徴・備考 |
| アルミニウム (A5052) | 71 | 鉄の約1/3、同形状であれば変形量は3倍 |
| 超々ジュラルミン (A7075) | 70 | アルミ合金内で最高強度、ヤング率は同等 |
| 銅 (C1100) | 130 | 鉄の約0.6倍程度 |
| 真鍮 (C2801) | 100 | 黄銅、被削性に優れるが剛性は低い |
| チタン合金 (Ti-6Al-4V) | 110 | 鉄の約1/2、比強度(軽さと強さ)には優れるが、剛性は鉄に劣る |
樹脂・その他(Plastics/Ceramics)
樹脂材料は金属と比較してヤング率が低いため、構造設計時には注意が必要です。
| 材料名 | ヤング率 (GPa) | 特徴・備考 |
| ABS樹脂 | 1.9 | 汎用エンジニアリングプラスチック |
| ポリプロピレン (PP) | 1.1 | 柔軟性が高い |
| ポリアセタール (POM) | 2.7 | 機械的強度に優れ、摺動部品等に使用される |
| PEEK | 3.5 | 耐熱性・高強度のスーパーエンプラ |
| CFRP (炭素繊維) | 70 | 繊維配向により金属以上の剛性を発揮可能 |
| セラミックス (アルミナ) | 370 | 極めて高い剛性を持つ |
設計実務での活用法:ヤング率を使った「たわみ計算」
ヤング率を単なる物性値として終わらせず、設計計算に用いると、部材に荷重がかかった際の変形量(たわみ)を定量的に予測可能です。ここでは、設計実務で最も頻繁にモデル化される「片持ち梁」を例に解説します。
片持ち梁のたわみ計算式
構造力学の基本モデルである「片持ち梁(一端固定、他端自由)」の先端に集中荷重がかかる場合のたわみ量δ(デルタ)は、以下の式で求められます。
δ=(FL3)/3EI
F:荷重 (N)
L:梁の長さ (mm)
E:ヤング率 (MPa)
I:断面二次モーメント (mm4) ※断面形状に依存する幾何学的性質
この式において、E(ヤング率)は分母に位置しています。すなわち、ヤング率とたわみ量は反比例の関係にあり、ヤング率が2倍の材料を使えば、たわみ量は半分になるのです。
たわみ対策と「振動(共振)」対策
ヤング率は静的なたわみだけでなく、動的な振動の問題にも関わっています。
- たわみ対策として
上記の式からわかるように、たわみを減らすには、ヤング率か、断面二次モーメントを大きくするのが有効です。
- 振動(共振)対策として
部品の固有振動数は剛性(バネ定数)が高いほど高くなります。ヤング率の高い材料を選定すると、部品の固有振動数を上げ、モーターやエンジンなどの外部振動との「共振」を回避しやすくなります。
「たわみすぎて困る」「振動でビビリが発生する」といったトラブルの際、ヤング率は解決の鍵となる特性です。
計算シミュレーション例
以下の条件下で、材質によるたわみの違いを検証します。
条件: 長さL=100 mm、断面 10 mm×10 mm の角棒の先端に、100 N(約10 kg)の荷重。
まず、正方形断面の断面二次モーメントIを算出します。
I =(bh3 )/12=10×103/12=833.3 mm4
この数値を基に、鉄とアルミの変形量を比較します。
| 項目 | 鉄 (SS400) | アルミ (A5052) |
| ヤング率(MPa) | 206,000 | 71,000 |
| 計算式 | 100×1003/(3×206000×833.3) | 100×1003/(3×71000×833.3) |
| たわみ量 | 約0.19 mm | 約0.56 mm |
算出結果より、アルミは鉄に対して約3倍変形しやすいことが示されました。これが設計上の剛性差となります。
ヤング率が変化する条件(注意点)
ヤング率は材料固有の定数であり、基本的に変化しないものとして扱われます。しかし、実際の設計環境では、以下の条件によって数値が変動することを考慮しなければなりません。
温度による変化
ヤング率は温度の影響を強く受けます。一般に、温度が上昇すると原子間の結合力が弱まるため、材料は柔らかくなりヤング率は低下します。
- 鉄鋼材料:常温では約206 GPaですが、高温になると徐々に低下し、400℃付近では約2/3まで低下する場合があります。
- 樹脂材料:金属に比べて熱に弱く、数十度程度の温度上昇でも剛性が低下します。特にガラス転移点を超えると、柔らかくなるため注意が必要です。
高温環境下になる炉内設備や、エンジンの排気周辺部品を設計する際は、常温時のカタログ値(代表値)を使ってはいけません。必ず「使用温度域におけるヤング率」のデータを参照して計算を行いましょう。
材料の向き(異方性)による変化
一般的な金属材料(鉄やアルミ)は、どの方向から力を加えてもヤング率はほぼ同じであり、これを「等方性材料」と呼びます。しかし、材料の内部構造によっては、方向によって硬さが異なる「異方性」を示す場合があります。
- 圧延金属:金属でも強い圧延加工を受けた薄板などは、圧延方向(L方向)とそれ以外でわずかにヤング率が異なる場合があります(通常設計では無視できる範囲が多いです)。
- 繊維強化プラスチック(CFRP/GFRP):最も注意が必要です。繊維が並んでいる方向には金属並みの高い剛性を発揮しますが、繊維と直角の方向には樹脂並みの低剛性となります。
- 射出成形品:樹脂にガラス繊維を混ぜた材料では、樹脂が金型内を流れる方向(配向)に繊維が並ぶため、流動方向と直角方向で剛性に差が出ます。
樹脂や複合材料を使用する場合、「カタログ値はどの方向のデータか?」を確認し、荷重がかかる方向に対して適切な強度が確保できているかを慎重に検討しましょう。
まとめ
ヤング率(縦弾性係数)は、材料の「変形しにくさ(剛性)」を示す固有の物性値であり、「壊れにくさ(強度)」とは明確に区別すべき特性です。本記事では、フックの法則に基づく基礎定義から、実務的な単位換算、さらには「ハイテン材を使っても剛性は向上しない」という設計者が陥りやすい落とし穴まで解説しました。
設計実務においては、片持ち梁の計算式を用いた定量的なたわみ予測や、固有振動数の制御による共振対策が不可欠です。また、数値は常に一定ではなく、高温環境下での低下や、樹脂・複合材料における異方性といった変動要因を考慮することも、トラブル回避の鍵となります。
ヤング率は、構造設計の品質を根幹から支える特性です。本記事で紹介した知識を活かし、カタログ値の表面的な確認にとどまらない、論理的で信頼性の高い材料選定と構造設計を実現してください。






